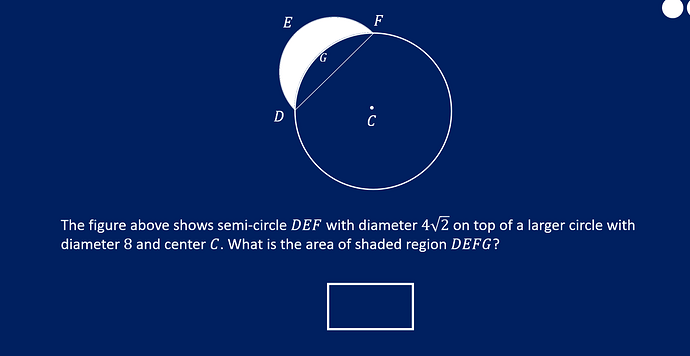
How can we be sure that the C piece is a right traingle? There is no information on the angle that is formed by DF to the centre given in the question. Someone please shed some light one this. I feel like I am missing something here.
How can we know for sure, that its a right angle triangle?
TIA
Question?
I got it from Greg anyway.
DF = 4 \sqrt 2, DC = CF = 4. That’s definitely a 45-45-90 right triangle.
Do we just do (Area of SemiCircle - Ar. of Segment ) ?
Yes, and you can find the segment area by taking (area of 90 degree arc - area of right angled triangle)
Thats the part I am confused. How can we form a relation from the three sides that it is a right triangle? Do we do pythagoras theorem to calculate whether the three sides satisfy the equation and consider it as right triangle?
Join DC, CF and DF. You get a triangle with lengths 4\sqrt 2 (hypotenuse), 4 and 4. What is that? A 45-45-90 right angled triangle. You can confirm by using the Pythagorean theorem (so it’s kind of an inverse).
It’s a property of triangle inscribed in circle. If the base equals the length of diameter and the triangle vertices is at circle circumference then the angle is always 90 degree.