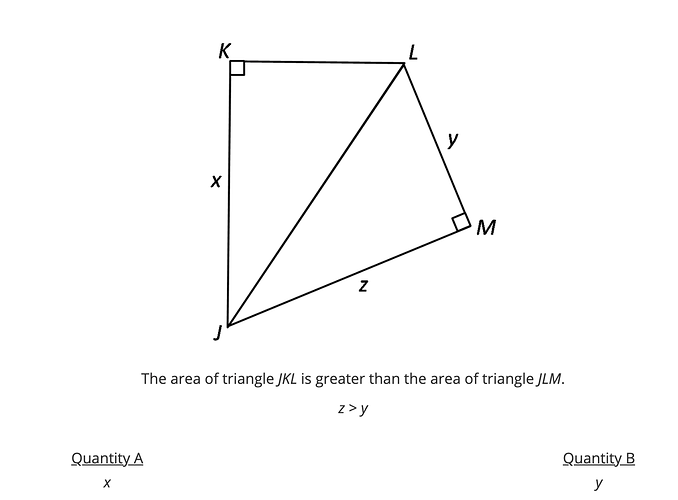
Can someone help me with this question ?
Hey I think the answer is D, now as both of these triangles share the same hypotenuse…(1)
Let us assume z=3,y=4, then hypotenuse=5
Also
Since its area(∆JKL) > area(∆JLM)
x(KL)>3(4)…(2)
(right angle triangle height * base formula)
So based on these 2 conditions, in ∆JKL, 2 cases can happen
1.my x must be >4 and KL <3, thereby solving the 2 conditions
2.or KL>4 and x< 3
Since both of these cases are possible, where in one case x >y and less than y in other,we don’t have enough information to answer and so we choose D
Correct answer is given as A
JL = \sqrt{y^2 + z^2}. This means that
KL = \sqrt{JL^2 - JK^2} = \sqrt{y^2 + z^2 - x^2}
It’s given that the area of JKL is greater than the area of JLM. This means that
\frac{1}{2}(\sqrt{y^2 + z^2 - x^2} \times x) > \frac{yz}{2}
\sqrt{y^2 + z^2 - x^2} \times x > yz
As z > y,
\sqrt{y^2 + z^2 - x^2} \times x > y^2
(z > y)
\sqrt{z^2 + z^2 - x^2} \times x > y^2
(\sqrt{z^2 + z^2} > \sqrt{z^2 + z^2 - x^2})
\sqrt{y^2 + z^2} \times x > y^2
x > y