I searched the forums to make sure this isn’t already answered. I’m stuck.
2 month study plan, week 2 day 5
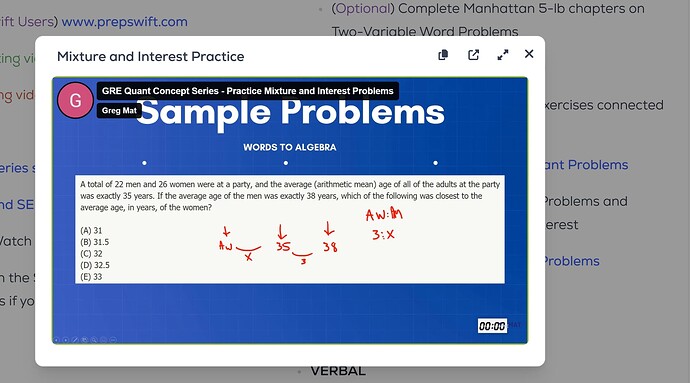
complete mixture and interest problems practice video
timestamp(h:m:s) 00:49:00
“everyone agrees that ratio of Women to Men is 3 to x right?”
I don’t know why we know W:M = 3:x
Couldn’t W:M = x:3, if x>3?
At 49:03 in this video…
I don’t know how we can determine if 3:x or x:3 is correct without knowing if x>3 or x<3.
I don’t know how we can determine if x>3 or x<3 in this problem.
Are my explanation, logic, and rule sets below missing things?
According to this shortcut method, the following rules applied
Rule 1: With counts or percents, When A>B
ratio A:B = greater:lesser
Rule 2.1: When |%(A+B)-%(A)|<|%(A+B)-%(B)|,
ratio A:B = greater:lesser
Rule 2.2: |avg(A+B)-avg(A)|<|avg(A+B)-avg(B)|,
ratio A:B = greater:lesser
Let A = W, let B = M
In this case, we know W > M, but we don’t know that 3 will be the higher number
The rules and given info don’t seem to allow this shortcut method to work
Given 1: count(W)>count(M). therefore ratio of W:M = greater#:lesser#
Given 2: distance |avg(W+M)-avg(M)| = 3
Given 3: ratio W:M = 3:x or x:3
per rule 2.2, If x>3, then W:M = 3:x
per rule 2.2, If x<3, then W:M = x:3
we need to know if x > or < 3
Is there another rule or method I’m not seeing being applied to in this case to verify if W:M = 3:x or x:3?
------My Solution------
Instead, the only method I found to work is using the equation Avg*Count = Sum, setting avg(W) as variable x then solving
{Avg(W)*Count(W) + Sum(M)} / Count(W+M) = Avg(W+M) and solving from there to find avg(W)