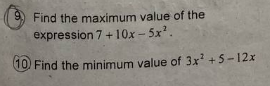
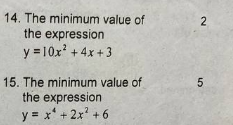
Can someone help me how to solve the above problems,
and are the above “valid” GRE problems (as i found a method that requires calculus to solve the above)
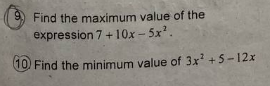
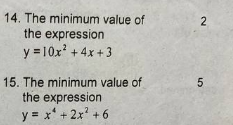
Can someone help me how to solve the above problems,
and are the above “valid” GRE problems (as i found a method that requires calculus to solve the above)
See the first question of the GRE Power Hour held on May 28th. Calculus is not needed, but can also be used.
Thanks for the reply, the problem i am facing is that the x^2 term has a coefficient which is NOT a perfect square, does ETS usually not ask questions having such coefficients?
Also can you help me how to find the maximum value?
Thanks in advance
It’s similar. So, for (9), 10x - 5x^2 + 7 is - (5x^2 - 10x - 7), or -5(x^2 - 2x - 7/5). You can complete the square as -5(x^2 - 2x + 1 - (7/5 + 1)), or 5(12/5 - (x - 1)^2). Hence the answer is 5 \times 12/5 = 12.
While probably on the harder side, questions asking you to complete the square or use the quadratic formula are fair game, as they do not require explicit calculus knowledge.
Thanks that cleared my doubt!