Formally: use calculus.
Using GRE techniques: can we make use of another sequence?
Which sequence can we make use of?
Say something like 1/7, 1/7, 1/7, … ?
I don’t know how to use 1/7, 1/7, 1/7 but when I write out the sequence we see that a1+a50 is just barely over 1. Then a2+a49 is just barely over 1/2.
The largest number we will have is just barely greater than one then 1/2, 1/3, 1/4 etc. Even with 50 numbers they don’t add up to more than 7 but I can’t figure out how to prove it with the sequence.
Curious for more of a hint here Leaderboard as I’d love to figure this one out.
Notice that
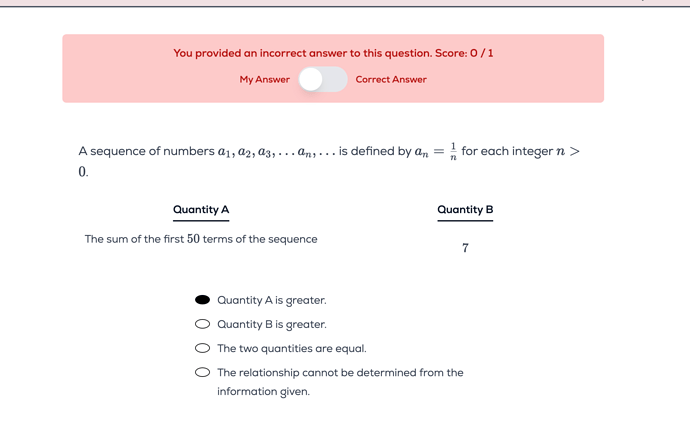
1/7 + 1/7 + 1/7 + … + 1/7 = 50/7 which is just a hair greater than Quantity B.
Take a look at the original sequence. Only 7 terms are greater than 1/7. The rest are less than that. Does that give you a hint?
[Hint: you could also bound this to 1/8 + 1/8 + … + . But that’s a little bit more work]
Are we using 1/7 because quantity B is 7?
More of the fact that the sum of the first fifty terms of the sequence 1/7, 1/7, 1/7 … is just over 7.
That makes sense but doesn’t feel intuitive to me. My strategy was to add up first and last, second and forty ninth, and so on and sum to find out of A was greater than or less than 7. But those fractions were impossible to work with so I was guessing at best.