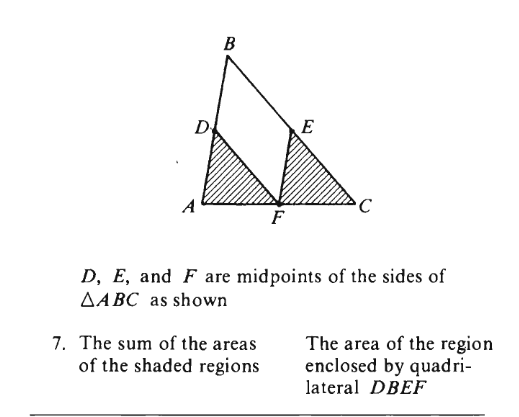
Mid Point theorem:
Statement: The midpoint theorem states that the line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of the third side.
Join D to E.
Now, by Mid-point theorem :
DE = \frac{1}{2}AC
DF = \frac{1}{2}BC
EF = \frac{1}{2}BA
Therefore, \frac{DE}{AC} =\frac{DF}{BC}= \frac{EF}{BA}= \frac{1}{2}
Triangle DEF \sim Triangle ABC
Hence, \dfrac{\text{area of triangle DEF}}{\text{area of triangle ABC}} = \frac{DE^2} {AC^2} = \frac{1}{4}
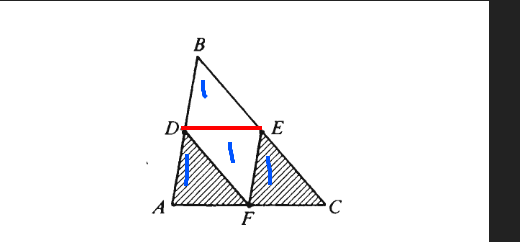
Hence, each small triangle has a area ratio of 1 w.r.t. big triangle ABC i.e. each small triangle has an area of 1 and we got 4 of those small triangle which when combined make big triangle ABC which has area of 4 (1+1+1+1)
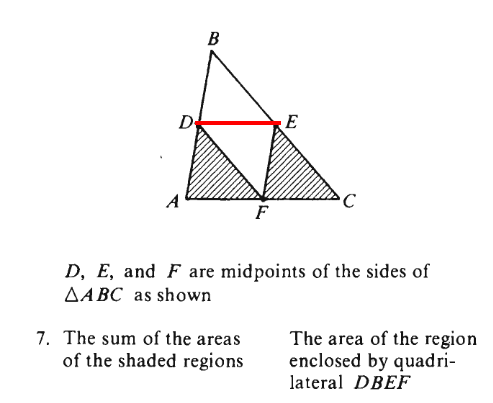
Option A:
shaded region = 2 small triangle with ratio of 1 = 1 + 1 = 2
Option B:
Area of quad. DBEF which is made up of two small triangle DBE and DEF which also have a area ratio of 1 hence , 1+1 = 2
Qty A = Qty B
OR
Because D E and F are mid-points then they will divide the side into two equal half’s. Can assume in QtyA that as the base is the same (mid-point) and the height is the same ; the two trianlges will each have the same area . Similary, for Qty B and then prove Qty A = Qty B