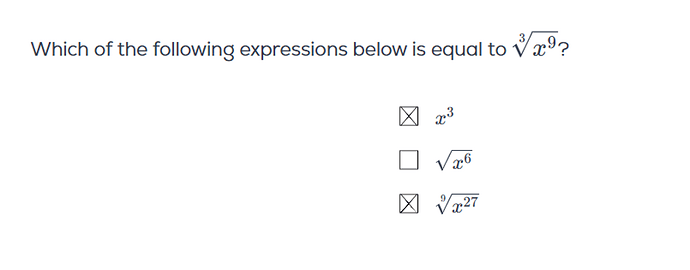Can someone please explain the negative and positive roots on the GRE.
1)Greg said to consider that whenever “principal root” would be present we always take positive root. Means √9 = 3 only, not -3
2) Another rule is x^2 = 9 means x = 3, x = -3
3) Finally, √(x)^2 = 3 means x = 3, x = -3
However,
Yes, it’s a convention to make \sqrt{.} a function. This means that you can only have one y-value for each x value.
1) This should answer why \sqrt{9} = 3 only cuz otherwise it wouldn’t be a function (but rather something u call a multivalued function - this isn’t relevant so i’ll just leave it at that). As to which value we should choose (the negative or the positive one), we conventionally resort to working over the positive reals for obvious reasons.
2) x^2 = 9 still conforms to what we established earlier. Your possible misconception comes from the fact that \sqrt{x^2} = x, which is clearly false. For example, \sqrt{(-2)^2} \neq -2 so yeah this doesn’t hold for negative values of x. In actuality, we have that \boxed{\sqrt{x^2} = |x| \neq x}.
Using this to answer solve your example should yield:
x^2 = 9 \implies |x| = \sqrt{3}
3) This is exactly what i described in 2), so i’ll skip the reiteration.
The question on the image:
\sqrt{x^6} = |x^3| from our definition above if we consider x \mapsto x^3, which is clearly not equivalent to \sqrt[3]{x^9} = x^3
Does that mean my point (3) is wrong, and √x^2 = |x| only?
\sqrt{x^2} = |x| = 3 \implies x = \pm 3
