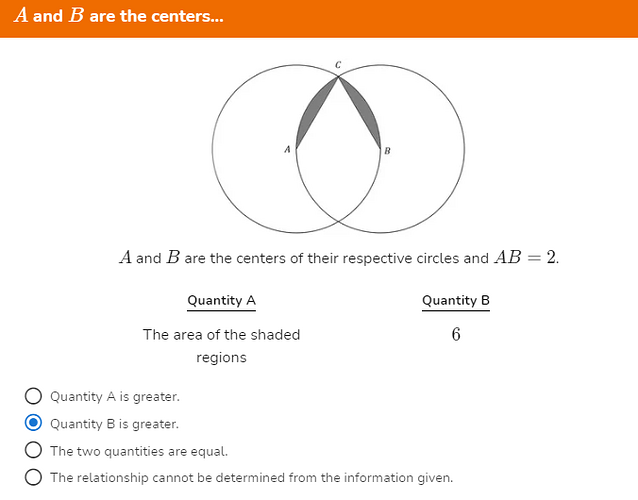
In this question A and B are given as the centers of both circles, that means AB is the radius of both circles. so the area of the whole circle (single) is 4pi. meaning the area of a quarter circle is pi. and the shaded region is within the quarter circle. which means the shaded region’s area is less than pi. then how can the answer be greater than 6
The answer given was A
How do you know that it’s a quarter circle?
The boundary of shaded line intersected the circle at point A and B which are the centers of the circle. the line joining A and B will be radius of both circle and if we draw tangent at the point A and B that will be perpendicular to the radius(i.e., AB), in doing so the entire shaded region will be between two perpendicular lines (intersecting at center) which means a quarter of the circle.
Triangle ABC is an equilateral triangle
The answer is 0.7, not 6. Hence you’re right, even though I don’t think it’s a quarter-circle myself. The answer is B.
(this can be easily shown by taking point D as the other intersecting point of the two circles and joining AD and BD. They form a 120 degree arc, and their area itself is less than 6, which means that the shaded area also must be less than 6.)
This has now been fixed, BTW.