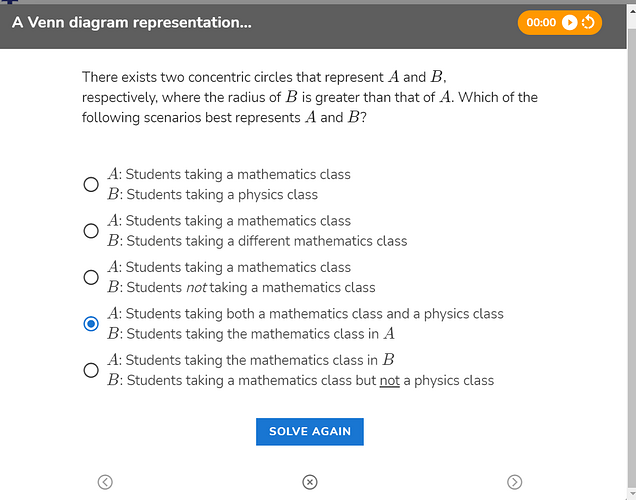
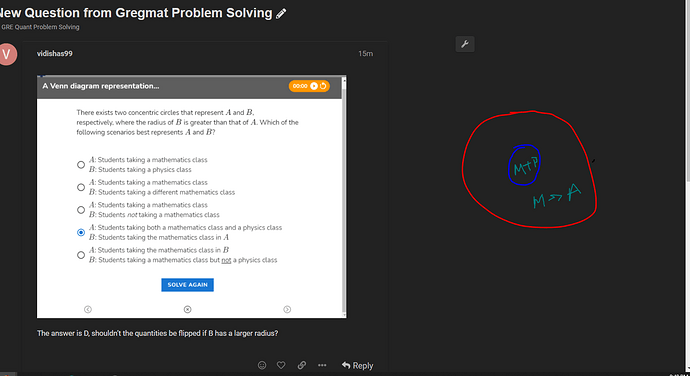
The answer is D, shouldn’t the quantities be flipped if B has a larger radius?
Because P+M should be greater than M alone ?
I meant that in the question it says
Radius of B is greater that A
But, the according to the answer the radius of A is greater than B
Yes
It isn’t - A is a subset of B since it consists of all students who are taking two classes, not 1 (so B, but not A, would include those that are taking mathematics but not physics). Hence the radius of B should be greater than A.
I am confused about this, the statement can interpreted in two ways:
-
We have mathematics students in B, some of these mathematics students have opted for physics as well. In this case B would be the bigger circle and A would be the subset
In this interpretation, we are considering A to be P \cap M
(which is what I think you are trying to say) -
We can also interpret the statements as: A is a collection of Physics and Math students, some of the students in this collection have Math (B), so B is a subset of A
In this interpretation, we are considering A to be P \cup M
P \cap M is a subset of M, but M is a subset of P \cup M
According to the answer, statement 1 would be the correct interpretation
Could you explain why the second one is the wrong way to interpret the statement
It’s not some, but all for Maths.