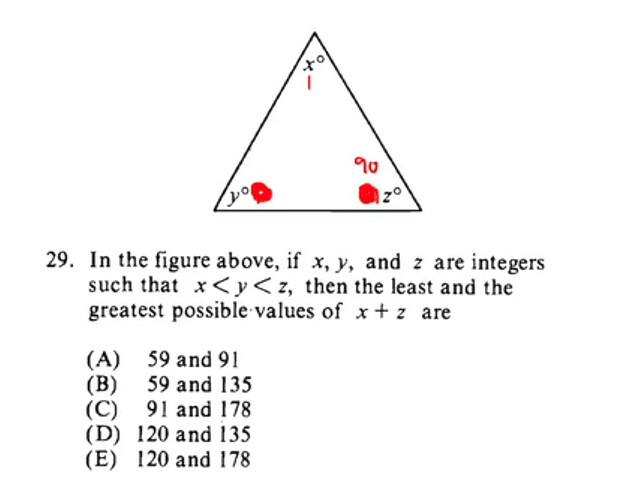
My question is: why can’t x=1, y=60, and z=119
thus x+z=120
and it also maintains the relation x<y<z
For the greatest value of x+z, you’d want to maximize x or z. We know x+y+z=180, So we can only play within that constraint. Let’s look at this problem as distributing 180 candies among 3 kids. Now we know we have to maximize the candies for x + z, so try distributing more candies to x. It means that the more you give to x the more you need to give y also (because y should have more candies than x), any candies that goes to y is a waste according to our expected results. So try maximizing z now. You can’t give all of the candies to z because x and y cannot be left without at least 1. So let’s distribute 1 candy to x and y each. But the problem says there should be lesser candies with x than y, so let’s give y one more. Now we have x=1, y=2, z=177. This is the maximum we can give z. So x+z = 178.
For the minimum, distribute the candies to all as equally as possible. Equal would be x=y=z=60. But x<y<z, so just snatch a candy from x and give it to z. x=59, y=60, z=61. Now to get the minimum of x and z, you should give y as many candies as possible. Can it further be minimised? Yes, just snatch 2 candies from x and give one to y and z (you should also give to z coz you have to maintain your inequality constraint). x=57, y=61, z=62. Keep doing it until x is almost out of candies, and voila! we’ve maximised y. and the value of x+z at this point will be your answer.
When you have considered x=1, y=60, and z=119, we get x+z=120. But is 120 the minimum? let’s try this. If I take one from z and give it to y, we’ll have x=1, y=61, and z=118. Now we’re still following all the constraints so x+z =119 now. This is definitely lesser than 120. But still, is this the minimum? Keep taking from z and adding to y, until you break the constraint y<z. For that value, you’ll get the minimum possible value for z and hence the minimum x+z