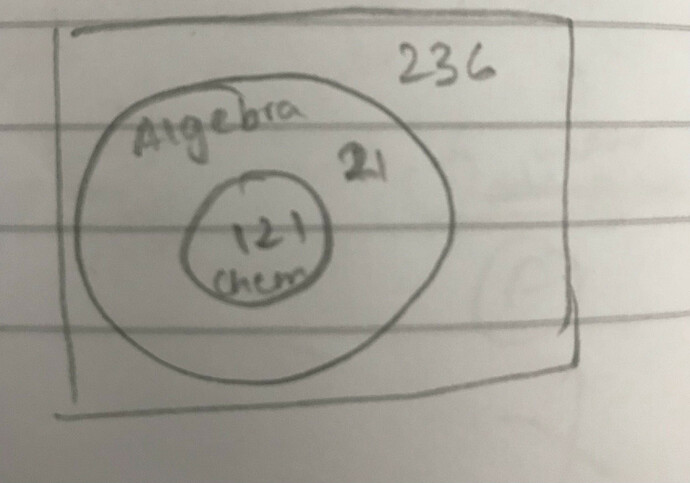
In the below question, if all 121 students take both chemistry and algebra then 21 (142-121) students have taken only algebra but this doesn’t add upto the total of 236.
The question does not say that everyone taking chemistry should take algebra. Just use the overlapping sets property: A \cap B = A + B - A \cup B. A, B and A \cup B are known. Maximise A \cap B.
But if I plug it in the equation, won’t I get 27? i.e. A and B = 142+121-236 = 27. But the answer is 121. If 121 students took both chemistry and algebra, then wouldn’t we have 21 that have taken only algebra but this won’t add upto 236. I interpreted the figure as:
What is the minimum possible value of A \cup B ? That’s 142.