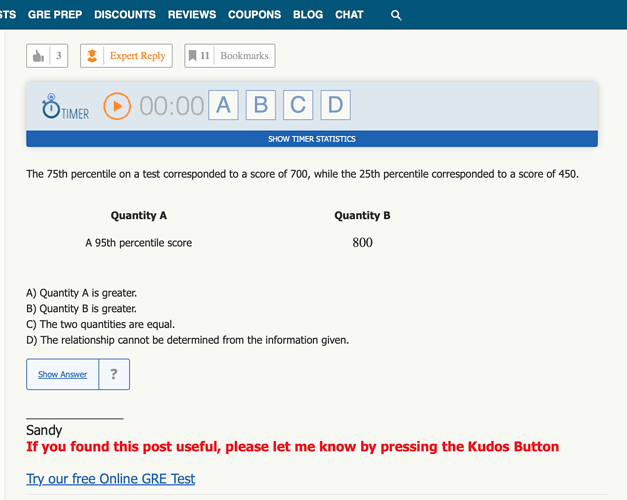
In this modified Manhattan 5-lb book question, the user asks whether – if the question had included a normal distribution – the answer would still be D (insufficient information to draw a conclusion).
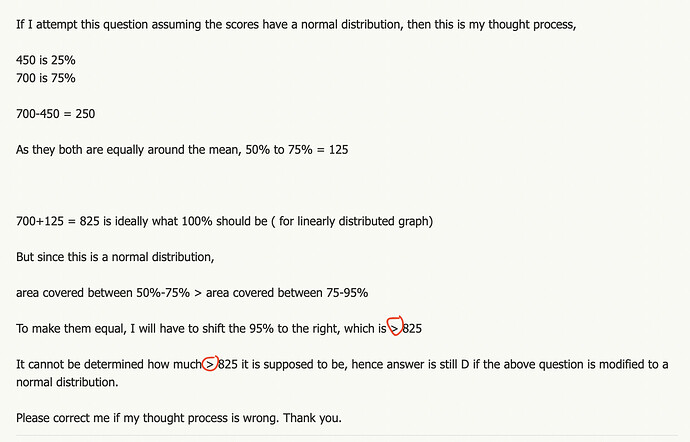
If this were a normal distribution, most of the values would be gathered about the mean; thus, to have the area between 50th and 75th percentile equal the area between 75th and 95th percentile, we would have to shift the 95th percentile to the right.
Doubt: “To make them equal, we would have to shift 95% to the right, which is > 825.”
Since in a linear distribution 825 would equal 100, why would the 95th percentile in a normal distribution be greater than 825? Shouldn’t it be less than 825 (since the area covered between the 75th and 95th percentiles is less than that covered between the 50th and 75th percentiles.)
This would also make more sense in terms of the final answer. If we were to know that the answer will be greater than 825, then the answer would be A. (not D). However, if the answer would be less than 825, then we wouldn’t have enough information to determine the relationship between Quantity A and Quantity B.