Polynomial under Root Sign and Absolute Value

GRE Quant Problem Solving
1

Hello,

I am currently going through the overwhlemed plan and had a question regarding polynomials under square roots, such as the two photos I have attached. Is it true that each time there is either an odd exponent (when attached to a variable) or a negative sign, the resulting term/expression will always only be the “absolute value”? Are there exceptions to this? And how can I find out when it is an exception?

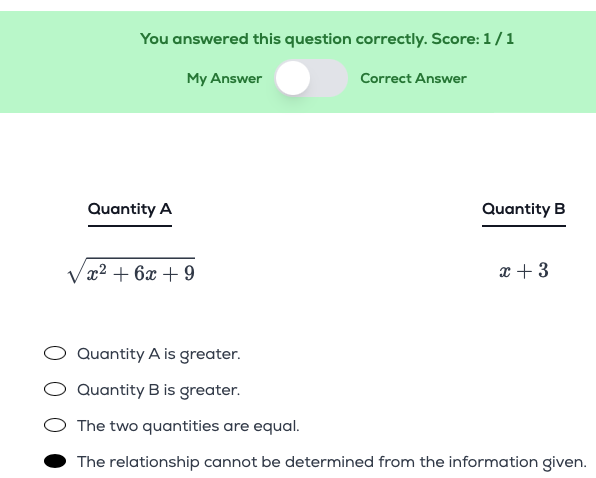
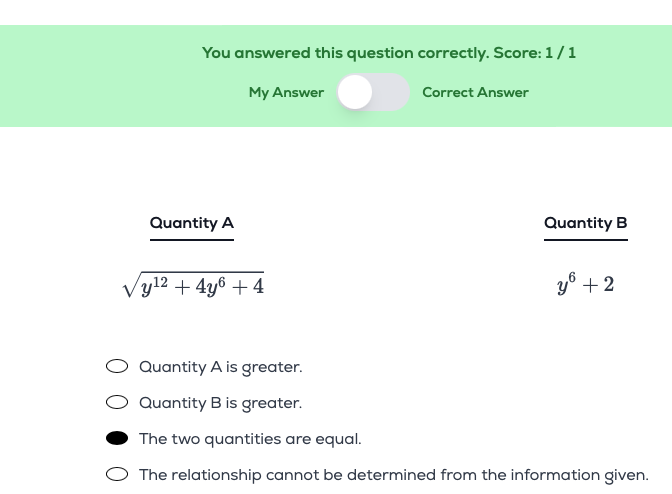
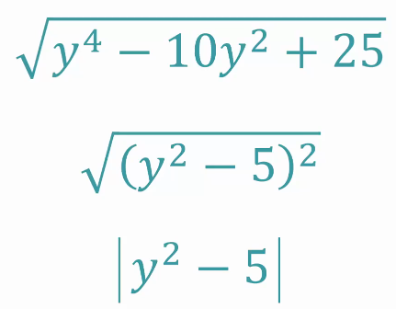
image
image
image

Have a great day!

2

\sqrt{x^2} = |x| by definition and you know that |x| = x only when x is non-negative. Try applying this knowledge/concept to your question.