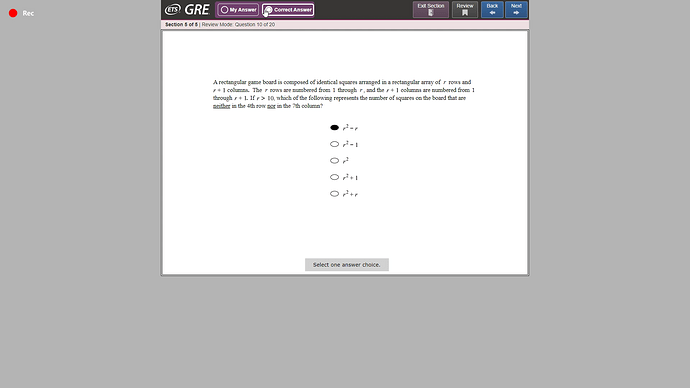
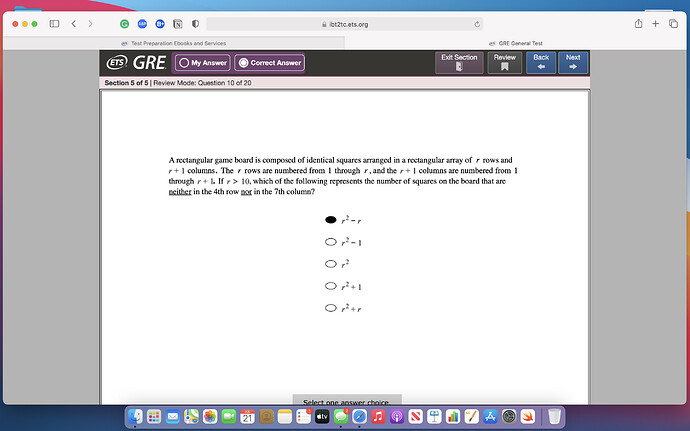
Hello, I couldn’t understand how to solve this question. Can someone help please?
Thanks 
Ignore the r > 10 condition (it’s symmetrical anyway). What happens if r = 3 (draw it)?
If r is 3, then we’d have 3 rows and 4 columns. The question wouldn’t apply itself then right?
It would. The condition r > 10 is arbitrary and the answer would not change if r < 10 (as long as r is at least 3).
Or just try with r = 11, though it will take a while longer.
Oh, okay. I think I got the solution. The total number of squares is r * (r + 1). But we want to exclude all boxes of 4th row and 7th row. So total number of boxes in 7th column would be r. So we subtract this from the above equation. It results in r2.
Next step would be to consider the 4th row. Here the total number of boxes would be r+1, but we have already removed one box while removing 7th row. So the total number of boxes that we’d have to remove would be r. So the resultant would be
r2 - r
We have a board of r*(r+1) dimensions.
There are a total of (r + 1) squares in any given row, and (r) squares in any given column.
Once you understand the above statements, you can solve it.
Total number of squares that are not in 4th row and not in 7th column is:
Total squares - squares in 4th row - squares in 7th column + 1
(Note: we do the +1 at the end because we removed it twice. One square is present in the 4th row and 7th column. So we undo that by adding 1)
r*(r+1) - (r + 1) - r + 1
= r^2 + r - r - 1 - r + 1
= r^2 - r
Thanks mate. Spot on. I approached the problem in the wrong way. So basically we are adding one because we are counting the number at index [4,7] twice. Thanks