PrepSwift Inscribed Polgyon Problems II Question 3

[user2135]

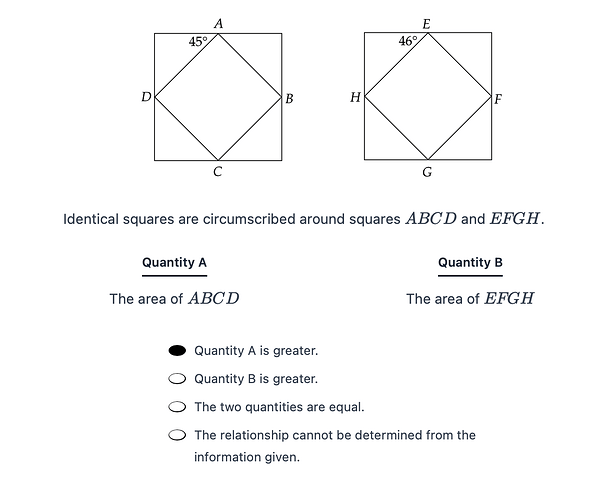
I can’t follow the solution at all.

My approach was the following:

In both diagrams:

There are identical squares being circumscribed around each square (ABCD and EFGH).

Aren’t there clear implications of different rotating angles?

Since the two inscribed squares are oriented differently with identical circumscribing squares:

The square with the smaller rotation angle (ABCD with 45) will have a larger area than the square rotated by 46.

This is because a larger rotation angle results in a longer diagonal for the inscribed square, which in turn means the side lengths of the inscribed square are shorter, reducing the area.

Another way to notice that the area of the square with the 46 rotation angle is smaller is due to the fact that the angle of the inscribed square is 88 instead of 90. In order to maximise the area of a polygon, it needs to be put in the most regular form which is a regular square with 90 degrees.

[cylverixxx]

Not sure i fully follow what your actual question is, but we can work with what you have for the meantime.

@user2135

Aren’t there clear implications of different rotating angles?

Rotating angle as in the labeled \theta in the diagram? If so, then yes because that’s clearly labeled in the image.

@user2135

This is because a larger rotation angle results in a longer diagonal for the inscribed square, which in turn means the side lengths of the inscribed square are shorter, reducing the area.

Uhh that’s self contradicting. You said longer diagonal for the inscribed square, so why should the side length decrease? You seem to have it reversed, because the diagonal of a square is \sqrt{2} \cdot \text{side length}, and so longer diagonal → longer side length.

@user2135

Another way to notice that the area of the square with the 46 rotation angle is smaller is due to the fact that the angle of the inscribed square is 88 instead of 90.

One of the internal angles can not be 88^{\circ} because it wouldn’t be a square then.

All squares are rectangles and all rectangles have equal internal angles (90^{\circ} each).