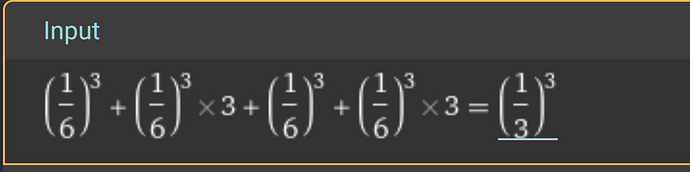This might be a very foundational level question. I’m having a hard time understanding when to use probability + Combinatorics and when it is just probability. For example this question from Tickbox quiz: If a fair 6-sided die is rolled six times, what is the probability that a 5 appears exactly twice in the first three rolls, and either 1 or 2 appears in each of the remaining three rolls of the die?
In the solution video, greg calculates the probabilty by multiplying the probabilty of two 5s and 1 not 5 with the number of arrangements possible using combinatrics. But for the second part the probabilty is just the product of probabilities of each occurence of 1 or 2? Why did we not use combinatrics here? Wouldn’t this also call for multiple arrangements like 111, 122, 121 and so on?
\left(\frac 13\right)^3 accounts for all arrangements of 1 and 2.
If that’s not convincing then I’ll just go the route of doing the actual casework for you:
Case 1: 111 → \left(\frac 16\right)^3
Case 2: 121 → \left(\frac 16\right)^3 \cdot 3
Case 3: 122 → \left(\frac 16\right)^3 \cdot 3
Case 4: 222 → \left(\frac 16\right)^3
The sum of all cases would then be:
Is there a way to calculate this using the factorial formula. like (1/3)^3 * 3! ? (I don’t know how to get the number of repeats though)
1/3 gives you all cases where each of the three numbers is a 1 or a 2. I don’t see why you would multiply by 3! again when it already accounts for all such cases. Maybe you should reread the thing i wrote above.
1 Like