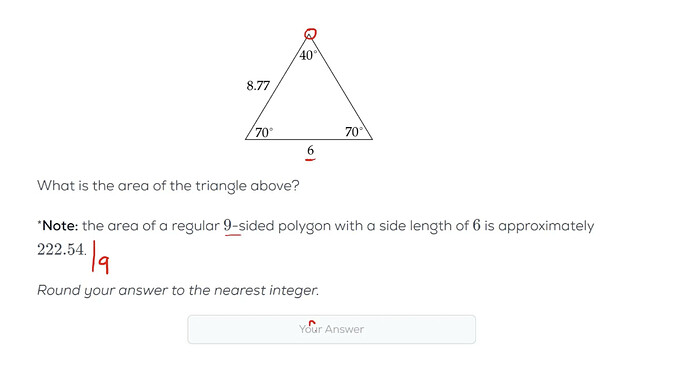
Hi. Would someone be able to explain why we are dividing the total area for a regular 9-sided polygon by 9 to get the area of the given figure? The given figure is not a regular polygon (i.e. it is not an equilateral triangle), so how can we determine that the height is the same as the regular nine-sided polygon? Maybe, I am missing something.
Whoever can solve this question, I declare the math god who will ace the GRE Quant section!
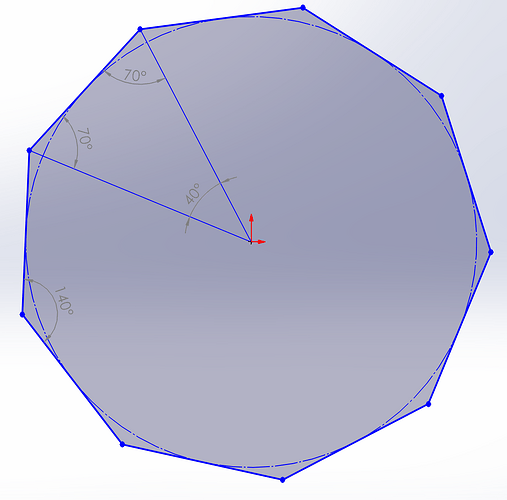
Try sketching the 9-sided polygon.
that does not solve the question. how can we calculate the area of polygon with uneven triangle?
The 9-sided regular polygon has 9 triangles of those form. They’ve given you the total area of the 9-sided polygon, so finding the area of one such triangle is straightforward.
The triangle they are showing is not the triangle that forms from a 9 sided polygon. The triangle that forms with 9 sided regular polygon has 40,40 and 100 angles.
The triangle they are showing in the question has 70,70,40. This triangle is not formed from a 9 sided regular polygon. The triangle that forms with 9 sided regular polygon has 40,40 and 100 angles Because. The angles inside will be 140 from the formula [n-2]*180/9=140. so the outside angle will be 40. And as this will be a isosceles triangle. [40,40,100].
140 is NOT the central angle. It’s just the interior angles which are bisected so 70 each. The central angle is just 360/9 = 40. So you have two 70’s and one 40
To elucidate on my previous comment, have a look at what 140 actually represents. The central angle is the angle that’s different in the isosceles triangle concerned.
i understand it now. Thanks