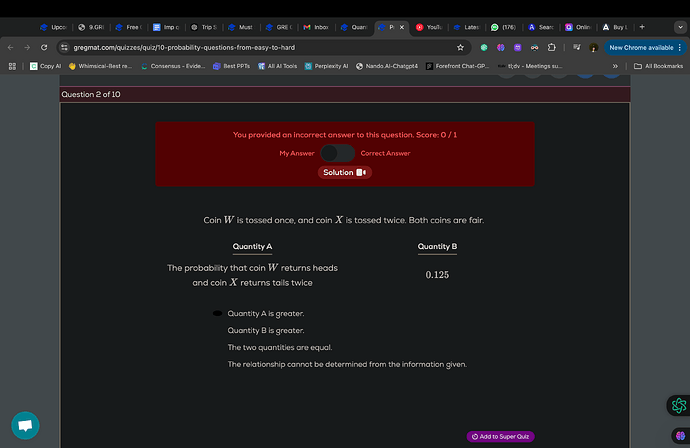
I am a bit confused as to why we didn’t multiply 1/8 with 3!/2! because it could be possible right that coin X is flipped first and then coin coin W or vice versa. The question doesn’t specify the order of the outcomes so why are we not multiplying with 3!/2! because in other coin related questions we have taken into account the order of the flip. I am not able to understand why it doesn’t matter here?
There is nothing in the question to indicate that it matters whether coin W or X is flipped first or not.
but in a lot of other questions too, it doesn’t explicitly mention that. For eg, in coin toss problems, when it says a coin is flipped 4 times, find the probability of at least 2 heads. There we do this to account for different arrangements so I am still confused, why wouldn’t that be applicable here?
This is a nice question, but unfortunately at this “level” the only real answer is that it’s kinda philosophical. From considering the permutations, you have that all these three arrangements work: HTT, THT, and THH and then naturally you’d surmise that the order in which you flip the coins affects the probability. However, intuitively this should already seem off.
For example, suppose we flip W first and then X later, then our “good outcome” is HTT. Now, if we flip W last then the new “good outcome” is TTH, but this is just a change in perspective and doesn’t really affect the numbers. It’s essentially like requiring one of them to occur is indistinguishable from requiring the other to occur, to some extent.
If you’re willing to go up “one level”, I can give you a more convincing answer mathematically, but if you’re satisfied with this then that’s also sufficient.
I appreciate your explanation, but I’m still not entirely convinced because it feels like a similar logic could apply to other questions where the arrangement matters, even if it isn’t explicitly stated in the question. That said, I don’t think I’d be able to fully grasp a very advanced mathematical explanation, but I would still love to hear it and give it my best shot. If not, I suppose I’ll have to accept that the reasoning might not always be explicit.
It’s not. It should be accessible for you if you’ve done a bit of intro probability/stats.
To start off, you can imagine modelling this as a multivariate result. This would mean considering two experiments in parallel where the corresponding random variables are (W,X) where W = (W_1) is the single toss of coin W and (X_1, X_2) are the two tosses of coin X. For brevity, we’ll assume that heads = 1 and tails = 0. Given this, you have (W_1, X_1, X_2) maps into \{0,1\}^3 with uniform distribution (because all coins are independent and fair). Thus, the event that W returns heads, and X returns tails twice is precisely \{ (1,0,0) \} and there’s no permutation to consider.
The above is basically an answer to your question, but i’ll try to distill it down even more for you. Each coin has its own random variable and so we’re dealing with 3 random variables: W_1, X_1, and X_2. One experiment would then involve sampling one value of (W, X_1, X_2). Among all \{0,1\}^3 (this means all 3-element tuples with elements which are either 0 or 1), we want exactly (1,0,0). This is the only tuple which takes this value amongst the 7 other tuples. There’s no permutation occurring because the first one is always the output of W, the second one being the output of X_1, and the third one being the output of X_2. This is basically like if you have (x,y) = (1,2) then you know that x = 1 and y = 2, which you clearly don’t permute.
In fact, all the example problems you looked at where the “permutation” (different arrangements) are even concerned doesn’t involve swapping elements around in a tuple either. The setup for a binomial distribution (the problems where you consider “arrangements”) is modelled by bernoulli distributed independent X_1, X_2, ..., X_n. Suppose we have n fair coins then each random variable considers just the output of a single coin. Then what’s actually happening is that we define a new random variable X = X_1 + X_2 + \ldots + X_n. Thus, when we say something like “exactly 3 heads”, we’re looking at the event \{X = 3\}, which is given by a lot of tuples (because there’s different values each X_i's can take and still give X = 3).
Essentially, you’d count all the tuples which meet your requirement. Mathematically, it would look something like:
\{(x_1, x_2, ... , x_n) \in \{0,1\}^n: x_1 + x_2 + ... + x_n= k \}.
Put in easier to parse words: find all tuples such that when all their elements are summed we get a sum of k.
Tldr; you have (W_1, X_1, X_2) and if heads = 1 & tails = 0 then you’re looking for a (1,0,0), which is 1 of the 8 of all possible 3-element tuple. You don’t permute and consider different arrangements cuz that makes no sense to do with random variables. Your other problems use a different setup whereby we’re trying to have the sum “mini random variables” equal a value we want. Hopefully, it’s somewhat clear how they’re two different things. In particular, your question here is asking for 1 tuple which takes a particular value; whereas, those other problems takes into consideration all tuples whose elements sum to what we/you want.