I am still somewhat stuck in this explanation on why if someone pulls a red marble one by one without replacement, the probability is the same. Isn’t for the first attempt, the probability of pulling out the first marble is 2/4 or 1/2 or 50% and if you don’t replace it, it’s 1/3 or 33%?
Isn’t for the first attempt, the probability of pulling out the first marble is 2/4 or 1/2 or 50% and if you don’t replace it, it’s 1/3 or 33%?
That’s true, but there’s no guarantee that will happen. There’s also the possibility that you didn’t pull out a red marble first time.
This is why we consider all the outcomes (all the different ways we can pull out all the marbles), and we realise it’s the same.
Thank you for weighing in, really appreciate the time taken to help me with this.
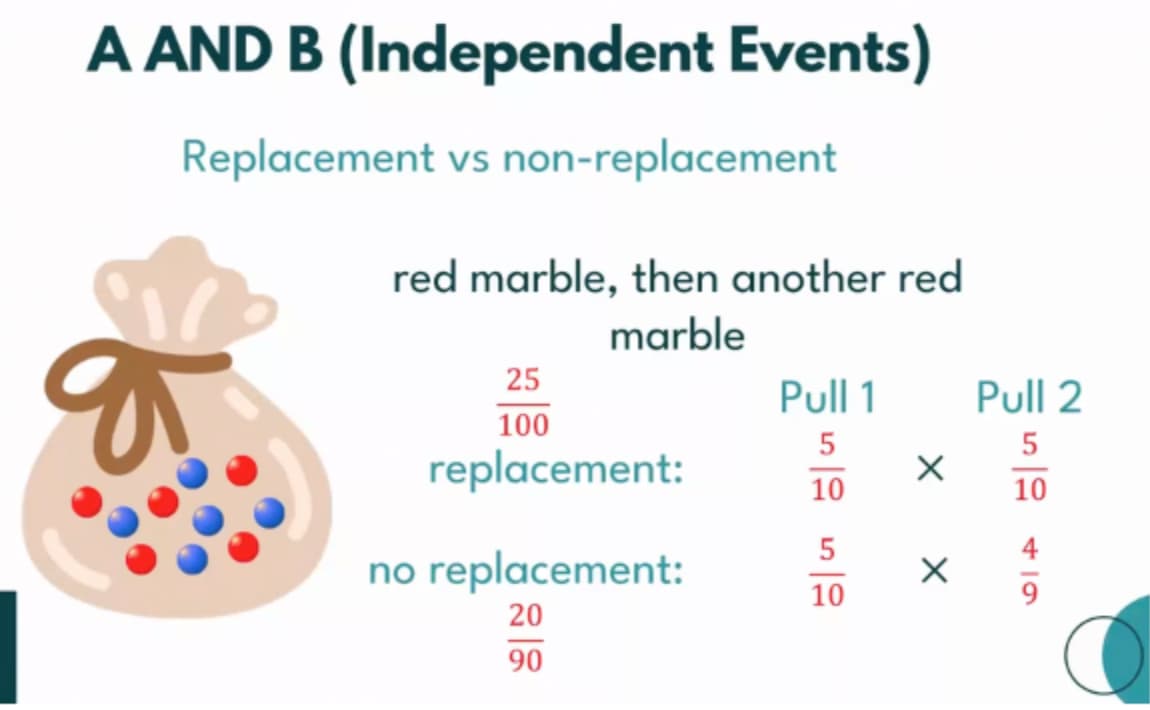
But considering the red marble point, wouldn’t that means sequence then matters? But it shouldn’t be, right? Because the probability is already counted in this scenario which is 1/4. Also, wouldn’t that somewhat contradict the example below? Sorry about that, still rather confused ![]()
The order does matter here, since we have to consider every different order in which the marbles can be pulled out.
We can rephrase the first question like this:
If we consider all the different orders in which the marbles can be pulled out, what is the probability that a Red is in the first position?
Also, wouldn’t that somewhat contradict the example below?
The example you posted is different, because it is 2 conditions:
- Red marble first
AND - Red marble second
In the first question it just means “red marble in first” or “red marble in second”, we don’t care where the other marbles are.