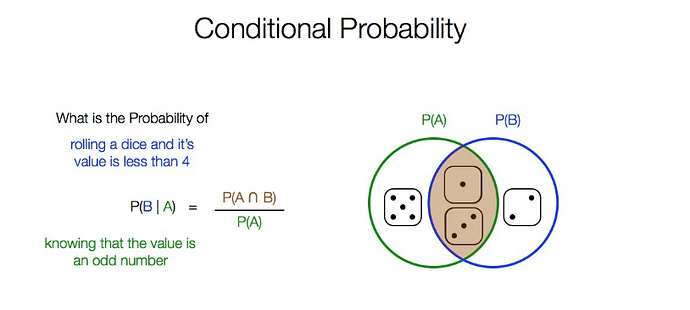
Let’s say we were to roll a dice once, and wanted to know the probability that the roll was less than 4 AND it was an odd number. These are not mutually exclusive events, so the probability of A and B should be P(A) * P(B) which is (1/2)*(1/2) = (1/4). But in reality, the probability here is 1/3. Why doesn’t the intersection formula work here? Thanks!
Because when you consider 1/2 * 1/2, you are also considering the dice roll value’5’ too.
Yes, it is an odd number, but it isn’t below 4.
So, you can read the question as ‘what is the probability that the roll is an odd number, given that it is below 4’
Now, since we know it has to below 4, and it has to be odd, the only numbers possible are: 1,3.
So that is basically 2 possible numbers out of the total 6 numbers on a dice.
That is: 2/6 = 1/3.
Hope this helps.
Ok, so in this example I got from YouTube, is the numerator they use in the equation the wrong formula? If what your describing is the proper process, then what is the point of dividing by P(A)? Hopefully my question makes sense, I am just trying to know definitively how to use the P(B | A) formula. Thanks!
Hi,
The formula in the youtube video is correct.
What the formula signifies is basically:
Numerator - probability of both events taking place together (Both A and B)
Denominator - total probability of the given event occurring.
So in simple terms, out of total possible of the given event A, how often does B also occur with A.
I see; but I guess that returns to my original question - why doesn’t the formula for the numerator yield the correct value, when that formula would typically calculate out to (1/2)*(1/2)?