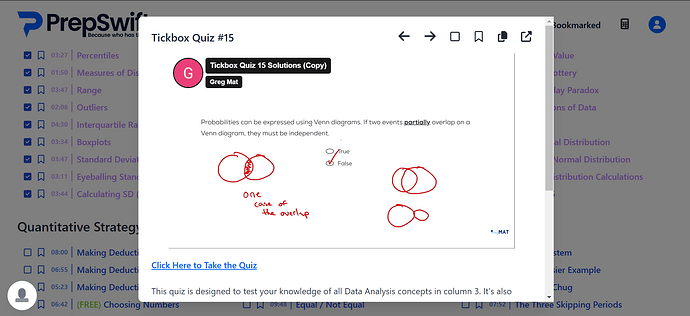
Here, the question is not about the “only partially overlap in venn-diagram must be independent” , the question is “partially overlap must be independent”. So, I think it is true, partially overlapping must be independent.
If partially overlap must not be independent then what’s the other case? Here, it’s not asked and discussed about the other cases of independent and not denoting the only case is partially overlapping, so how can we say false on this?
Two events are independent if their joint probability is equal to the product of the individual probabilities.
In particular:
P(A \cap B) = P(A) P(B)
It is not necessary that if there is overlap that the events must be independent.