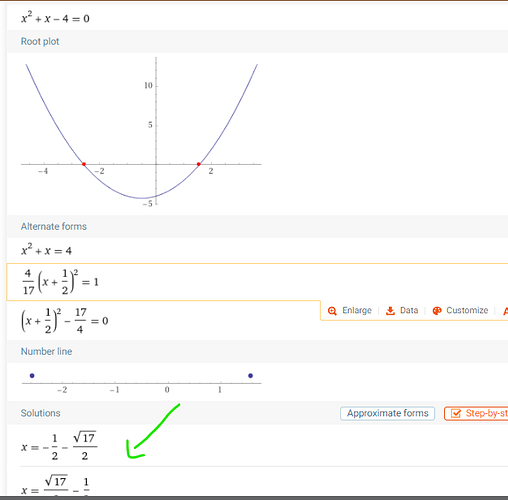
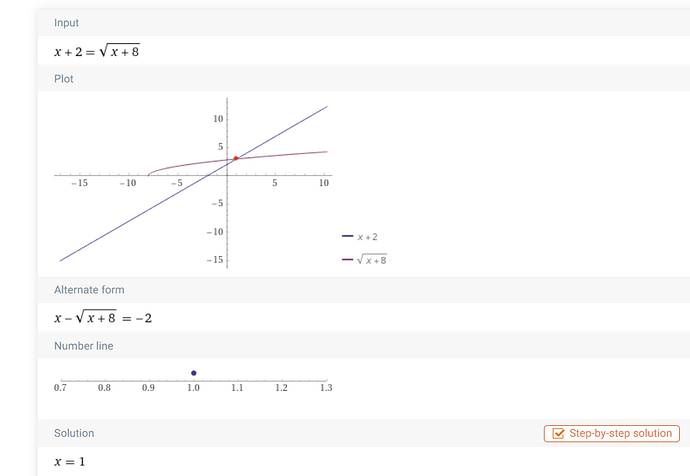
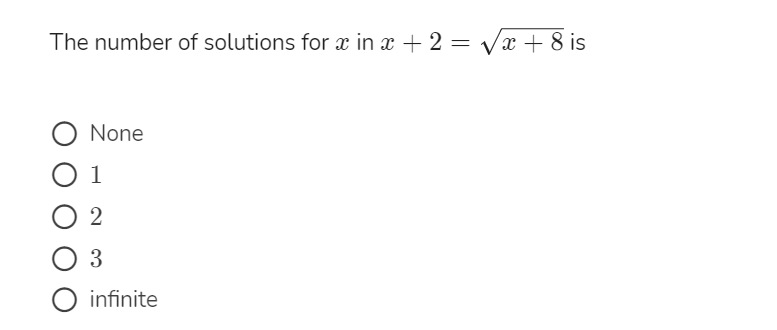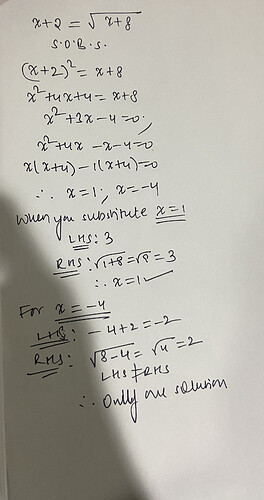Why the answer to this question is not 2 solutions?
The discriminant is b2-4ac and the answer is positive, which means there are 2 real solutions for this.
The simplified form of the equation is x2 + x-4 =0
Even @gregmat’s favoritas Wolfram-Alpha says there are 2 solutions for this eqn!
Kindly correct me if I’m wrong 
Can someone please explain why the answer is one?
x+2=square root(x+8) if squared on both sides and then solved as a polynomial equation gives 2 roots, 1 and -4
Am I doing something wrong?
Hi! I think the answer is 1 because you plug in each solution for x. So, for the equation x+2 = square root (x+8) with the solution 1 it would be; 1+2 = square root (1+8). 1+2 =3 and the square root of 1+8= 3.
Can someone explain how they solve this question? I did get an answer but apparently it is wrong. ( I got 2. ) I don’t quite understand the answer could be 1.
Ahh, okay. So I can’t consider -4 as a viable solution. Thank you, this makes sense!
The number of solutions in x+2 = sqrt(x+8)
When I solve it I get two solutions, x=1 and x=-4, what’s the logic as to why there is only 1 solution? Would appreciate an explanation, thank you!
