Quadrilaterals foundation quiz

GRE Quant Problem Solving
1

For this question, I used a slightly different approach. Since square is a special kind of rhombus, I used dimensions of the square to find out the side lengths and then the diagonals because I assumed that since square has a perfect symmetry and its area is maximum with a given parameter, it could be true that the sum of the diagonals is maximum. By fluke, I got the right answer but after researching online, I found out that this is not always true that square which is the special kind of rhombus always has the maximum sum of its diagonals and this is the reasoning I found online. So, I would be thankful if someone could validate this reasoning or if its incorrect, you could help me establish the fact that square really has the maximum sum of the diagonals. I am looking for a generalization of this logic.

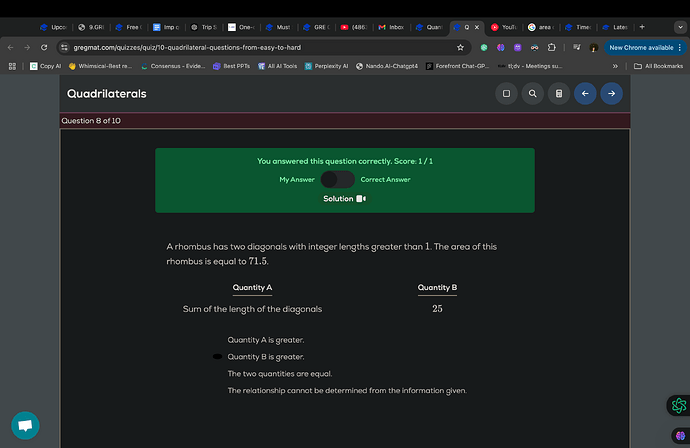
1. Can the largest rhombus be a square?

  • A square is a special case of a rhombus, where all sides are equal, and all angles are 90 degrees. While it maximizes symmetry, it does not always maximize the sum of diagonals for a given area.
  • The area of a rhombus is 1/2×d1×d2 and for a square d1 = d2, this simplifies to:Area of square=1/2×d^2. For a square with an area of 71.5, this gives:1/2×d^2=71.5 ⟹ d^2=143 ⟹ 11.96. So, the diagonals of this “square rhombus” would each be approximately 11.96, giving a sum of 11.96 + 11.96 = 23.92. This is slightly less than 25, and in this special case, it confirms Quantity B is greater.

2. Does this logic extend to other rhombuses?

  • Not all rhombuses are squares, and for a general rhombus with diagonals d1 and d2, the area is fixed by the condition: d1×d2=143. Any combination of d1 and d2 satisfying this equation with integer values (e.g., 11×13) will produce valid rhombuses. These cases show that a square is not necessarily the “largest” rhombus in terms of diagonal sums.

image
image2940×1912 404 KB

2

Why are u talking about a square when the question is about a rhombus lol. The whole idea is to maximize x + y given xy = 150, where x and y are integer diagonal lengths greater than 1.

I wouldn’t even use the word maximize cuz this question only demands of you to find the divisors of 143 and test like the only pair.

3

I was talking about a square here because I was trying to apply the extreme strategy logic used in QC to compare quantities which I had asked earlier for that Isosceles triangle question. I was wondering if square is a special kind of rhombus, could it possible that sum of the diagonals of the rhombus be maximum when it is a square. If that could be established, then we won’t have to check other combinations of the diagonals that would give us 143 as the product.So, the question is more on the lines if this logic is valid or not for other cases where let say it might not be very easy to find the divisors or it is too time taking.

4

Yeah but you’re doing an irrelevant problem, and just making the whole problem harder than it has to be.

No.

Let the two diagonals be x and y where x = 1000 and y = 0.001. then xy = 1. If we have that this is a square, we’d have that the diagonals sum to 2, but 1000.001 > 2.

5

Yeah, i think your point makes sense. I also tried other combinations and in a lot of cases non-square rhombus’s diagonals have a much greater sum. During the test I tried different combinations which all provided a sum lesser than quantity B (in case of square rhombus) and I thought maybe this is really some property that I am unaware about. Thanks for clarifying though.

6

In general, don’t use examples to make any kind of assertions. Proof by example isn’t a real thing.