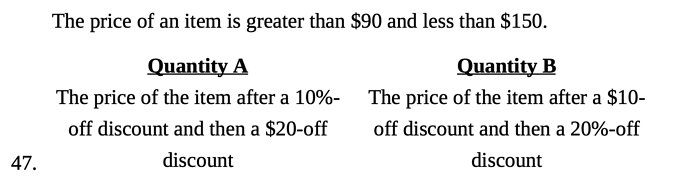Hi guys,
This question is from the Manhattan 5lb book, from the chapter on Percentages. The correct answer for this is D. While I get that substituting 2 different value will lead me to the same conclusion as the book, I want to understand the logic behind it as I may not always have the time to validate my answer with another value.
Thanks.
Let the price of the item be x
Quantity A says that the new price is equal to \frac{9}{10} x - 20, while according to Quantity B, it is \frac{8 (x - 10)}{10}. Compare the two:
\frac{9}{10} x - 20 = \frac{8 (x - 10)}{10}
\frac{9}{10} x - 20 = \frac{4x}{5} - 8
\frac{9}{10} x - \frac{4x}{5} = 12
\frac{x}{10} = 12
x = 120
This means that x = 120 is the point where Quantity A and B are the same, and beyond that, one of the two will be greater. Hence answer is D.
1 Like