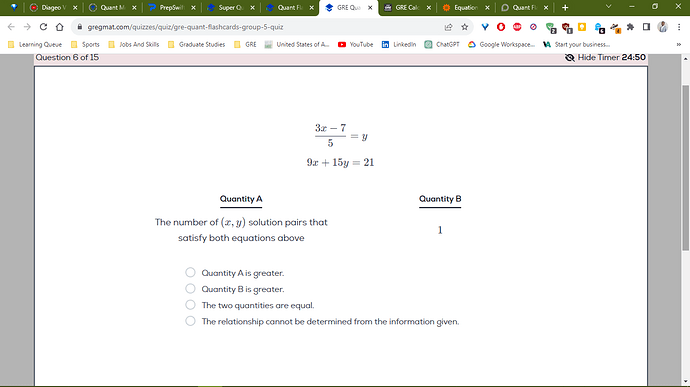
Should 9x + 15y = 21 and 9x - 15y = 21 have a solution set? The values I got using the elimination method (14/9 and 7/15) only satisfy the first solution.
0 solutions satisfy both equations since one is neg 15 and the other is pos 15 yet give the same result which is 21.
this set has no solutions ![]()
you’ll choose B since B is 1 and the solutions of x and y that would satisfy is 0.
1 > 0
Thank you. I chose B too. Surprisingly, Greg says there is one solution set. @Leaderboard, what do you think?
I don’t understand?
If you start with
\frac{3x - 7}{5} = y
we have
3x - 7 = 5y
3x - 5y = 7
Multiplying by 3, we have
9x - 15y = 21
So, notice that the second equation is 9x + 15y = 21. Adding the two equations, we’ll get
18x = 42
y = 0
This means that there indeed is one unique pair, making the correct option C.
(Note: if you got 9x + 15y = -21 instead, then there would be zero solutions, as you’re then saying that -21 = 21. That is not the case here)
Thank you.