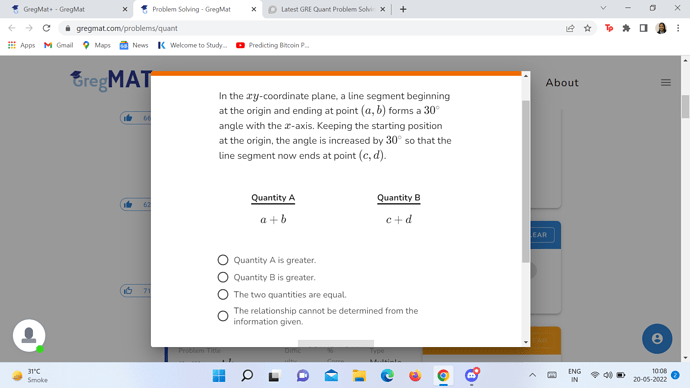
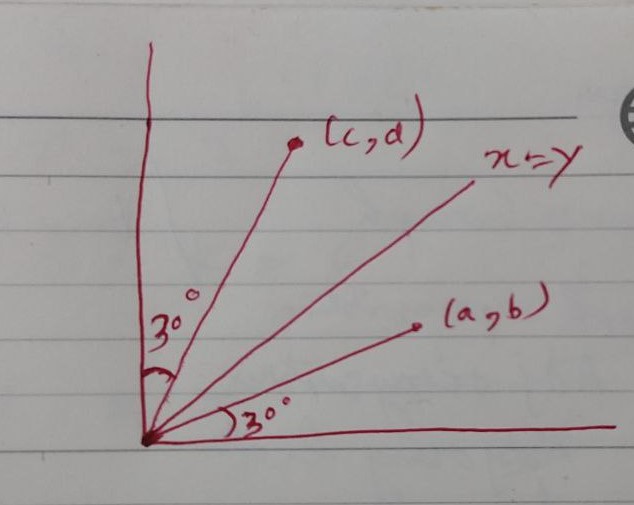
why (c,d) the y=x reflection of (a,b)?
If anyone could help, that would be great!
Thanks
Good question,
If you apply formula of distance between two formula, you will get length of segment equals to -
a ^ 2 + b ^ 2 or c ^ 2 + d ^ 2
Now, given segment length don’t change,
So,
a ^ 2 + b ^ 2 = c ^ 2 + d ^ 2 (if you use this method, you will get confused and end up ticking, D, which won’t be correct, as we have additional information in terms of angle)
Correct one
Now, we also know some trigonometry so, we know that Lsin30 = b, Lcos30 = a, & Lsin60 = d, Lcos60 = c.
Now, simply substitute values of sin and cos in the equation which will be
Lsin30 + Lcos30 = Lsin60 + Lcos60
L / 2 + sqrt(3)L / 2 = sqrt(3)L / 2 + L / 2
Answer is C
I got confused when the question stated only “keeping the starting position at the origin,” but nothing about the other end of the line segment. Technically I can manipulate the endpoint all I want as long as the final angle that the line makes with the x-axis is 60 degrees, right?
No you cant, note, they have said end point of line segment, means (a,b) and (c,d) are both fixed end points of the line.
Thanks for helping with trigonometry approach. Is there any other way to do the question?
x=y line makes angle of 45 degree with x axis and y axis.
line segment in first part makes 30 degree with x axis and 60 degree in the next part of question with x axis
so, in the second part of question, we can see it makes 30 degree angle with y axis (90-60 = 30).
This is how (c,d) is reflection of (a,b).
Hope this helps
add me tawkir.ahmed.018@gmail.com
wp: 01859099453