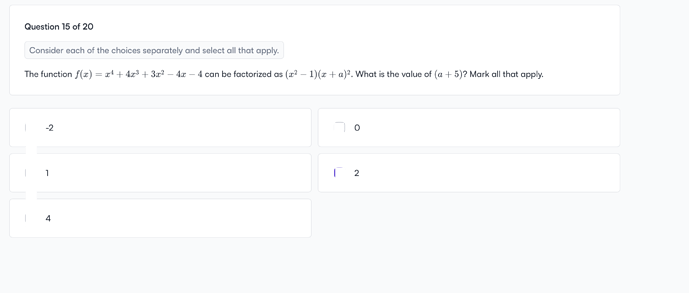
How do I solve the following problem?
What have you tried so far? The key is understanding the concept of factorization. They are already giving you the answer. When they say that x^4+4x^3+3x^2+4x-4 can be factorized as (x^2-1)(x^2+2ax+a^2), they are basically telling you that x^4+4x^3+3x^2+4x-4=(x^2-1)(x^2+2ax+a^2), so the only thing you need to do is expand the right hand side. Thus, you would get that:
x^4+4x^3+3x^2+4x-4=x^4+2ax+x^2a^2-x^2-2ax-a^2. Notice that the last term of the right hand side does not have an x, just like the number 4 of the left hand side. Thus, you can infer that a^2=4. Now you only need to determine whether a=2 or a=-2. What would your answer be then?
I’m getting a=2 as answer but that will make (a+5)=7 which is not present in the options.
My bad, got a 4x instead of -4x so we only need to correct that first
That doesn’t really answer my question.
To me looks like question is incorrect. Let’s confirm with @gregmat
That negative term -2a = 4 , tells a = -2 , but third degree coefficient 2a = 4 suggests a = 2. Now if consider it to be multi-select then answer could be either 7 or 3 . But there isn’t any such option. Is my approach correct? Can anyone confirm?
What’s the source of this question?
looks like its from scholarden judging from the UI but I can be wrong !(85% confident) @gregmat
Woflram says this is what it expands to when a = 2:
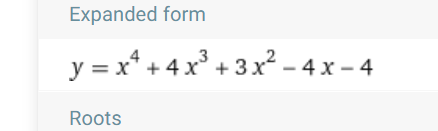
Which is what the original function says, so it looks like the answer 7 is missing.
Thanks I just needed that confirmation.