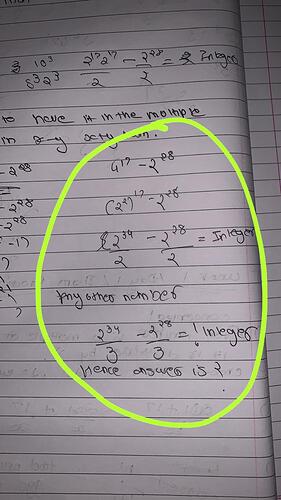Quant problem on finding greatest prime factors

[user3614]

Here is Gregs Solutions

What I was thinking was along the lines of:

According to my logic, the answer can only be 2 because the numerator is 2222…34times and 2 is the only prime factor that it is divisible by according to this representation

Would like to understand the gap in my conceptual knowledge that led to this error.

[HoldMyBeer]

(2^2)^{17}-2^{28} = 2^{28}(64-1) = 2^{28} \cdot3^2 \cdot 7^1

thus, greatest prime factor is 7

[user3614]

Sorry if was not clear with my question.
I get the approach that Greg has shown in the video. What I’m trying to understand is what is wrong with my approach which I have highlighted in the handwritten note, where I’m assuming 2^34/x - 2^28/x where x can only be 2 because both the numerators only have 2 in them.

[HoldMyBeer]

I think a simple example may solve your confusion :

Suppose we need to find greatest prime factor in the following problems and use your approach:

2^2 - 2^1= \frac{2^2}{2} - \frac{2}{2} = 2 \tag{1}

2^3-2^1 =\frac{2^3}{2} - \frac{2}{2} = 6 = 3\cdot 2 \tag{2}

As you can see the greatest prime factor is 2 in equation 1 but its 3 in equation 2.

Also , the answer you’re getting are multiple of 2’s {2 in equation 1 and 6 in equation 2 are multiples of 2 } while the question is asking about divisor {or factors} especially prime factors . You might want to google these terms to get a better understanding!

[user3614]

Hey thanks for the response, unfortunately, I can’t see equation 2 in your post.

This is what I’m seeing, can you post a screenshot of equation 2 maybe?

[HoldMyBeer]

[user3614]

Thanks for the explanation.
I guess what I construe from this is that if a number is a multiple of 2 then it does not mean that 2 is the only prime factor. The expression 2^x - 2^y can evaluate to a number where the factors can be prime numbers other than 2.
So the process would be to try and solve the expression first and find its prime factor representation, then look for the greatest prime factor.