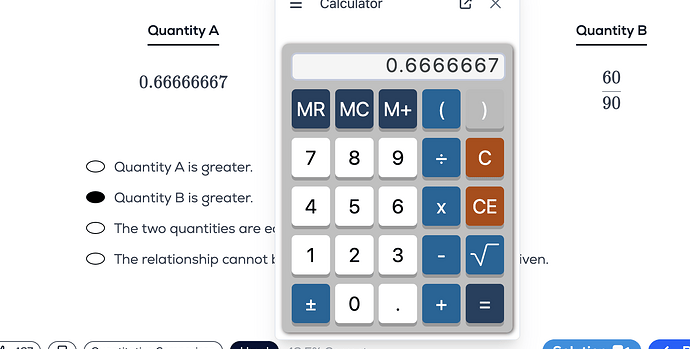
The calculator yields 0.6666667 for 2/3, which is a non-terminating fraction. Quantity A is 0.66666667, indicating that it has more sixes before the seven than Quantity B. Did we choose Quantity A because we know that Quantity B is a non-terminating fraction, and the calculator rounds up the last number. Can we apply this reasoning to all non-terminating fractions? If the calculator’s last digit is one greater, should we disregard it for non-terminating fractions?
For QC questions such as this, we should take into account that 2/3 will have a non-terminating decimal and disregard the calculator’s rounding. Hence, 2/3 0.66666667 is bigger than 0.66666667 2/3.
Actually the correct answer is A and not B that is why I asked and the reason given for A was because it has a seven and QB can never have a seven as it is a non-terminating fraction
Well yang’s “reasoning” is correct; he probably misspoke with the “ Hence, 2/3 is bigger than 0.66666667” tbh.
Anyhow, you can just imagine multiplying both quantifies by 10^8 (maybe express quantity B in decimals) and then by elementary school subtraction, the answer should be pretty evident.
No, I didn’t write that wrongly. I admit that I made a brain fart ![]()
I honestly thought 0.66666667 was smaller for some silly reason.
Thanks for correcting me!
haha no problem. Happens to all of us ![]()