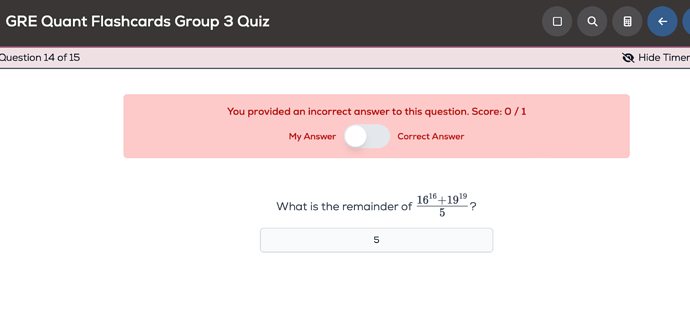
Why is the Answer 0 here? We are already dividing by 5 (16^1/5 R=1, 16^2/5 R=1 etc…) to get the remainder of 1 and 4 so why are we adding these 2 and then again dividing by 5?
The remainder of (a/b) + the remainder of (c/b) is not necessarily the same as the remainder of (a + c)/b. Can you see why?
I don’t see why… In another example of 77^7/5, we first took the remainder of 7^1/5 7^2/5 to find the pattern and then didn’t divide again by 5 to get the remainder? So I used the same approach above …
That’s because you’re finding the remainder of only one thing, that is, 7^{77} when divided by 5. Notice that you were finding the remainder of a sum in the original example.
Hi, so you’re trying to find the remainder when these two powers of 16 and 19 in the numerator are added. To assess that we’ll have to check patterns in the powers of 16 and 19 -
For 16, the powers have the following pattern:
(16)^1 = 16
(16)^2 = 256
(16)^3 = 4096
.
.
(The number always ends with a 6)
For 19:
(19)^1 = 19
(19)^2 = 361
(19)^3 = 6859
(19)^4 = 130321
.
.
(odd powers end with 9, and even powers end with 1)
Since the numerator in the question has an odd power of 19, it will end with a 9. And any power of 16 will end with a 6. So the sum of these two numbers will end with a 5 for sure, and any number that ends with a 5 is fully divisible by 5. Therefore, we’ll get the remainder as zero. Hope I was able to help