Need the solution to the below problem
Multiply both sides by
1/√5
Shouldn’t there be √5 +1= a/√5 +b ???
\frac{20}{5 - \sqrt{5}}*\frac{5 + \sqrt{5}}{5 + \sqrt{5}} = \frac{100 + 20\sqrt{5}}{25 - 5} = \frac{100 + 20\sqrt{5}}{20} = 5 + \sqrt{5}
Now, compare (5 + \sqrt{5}) to (a + b\sqrt{5})
a = 5
b = 1
a+b = 5+1 = 6
Ans. B
1 Like
Thanks a lot!
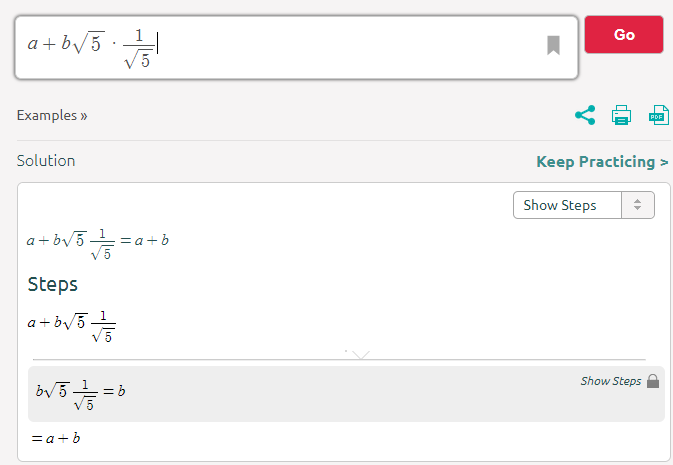
No
You are multiplying \frac{1}{\sqrt{5}} to only one of the terms
(a+b\sqrt{5}) * \frac{1}{\sqrt{5}} is going to give (\frac{a}{\sqrt{5}}+b)
Is it allowed to multiply only one term during Quantitative comparison?
Who knows , Is there a solution to this problem ?
Yes
I mean the video solution?
No, there isn’t at the moment
I think until Greg clears it people should follow your solution , I think I just got lucky
1 Like
What you did was
a + b\sqrt{5} \times \frac{1}{\sqrt{5}}
while what you really intended to do was
\left(a + b\sqrt{5} \right) \times \frac{1}{\sqrt{5}}
1 Like
Ahh , I see
Exactly