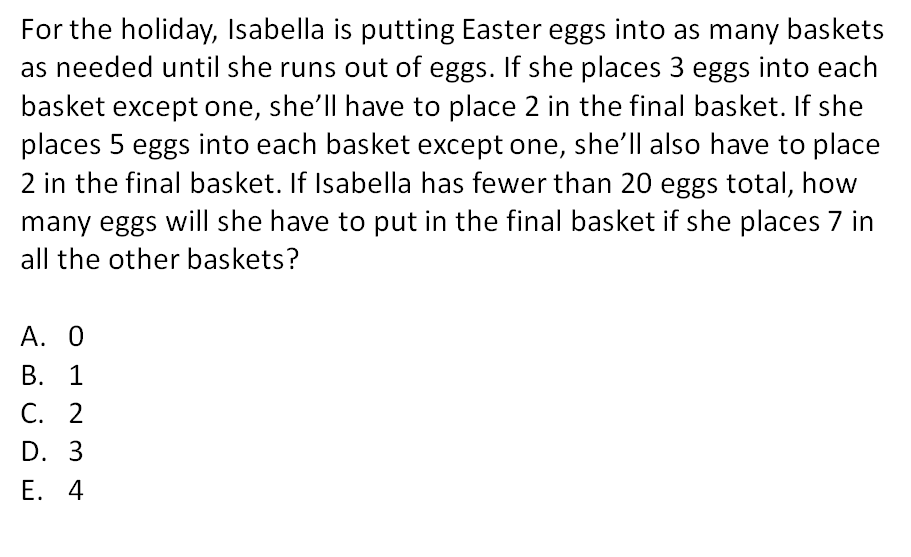I messed up the recording process with this class, so I said I would post the questions here:
Answer to 1st = 4
The ans for 2nd is 15& 60?
Can someone explain why 1 is 4?
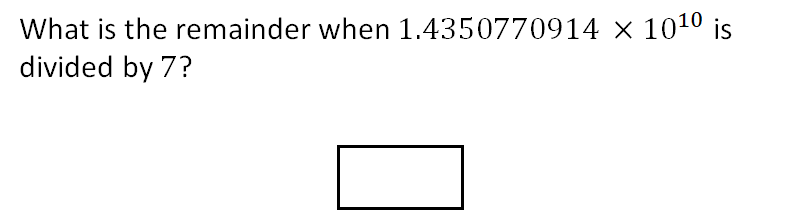
If you divide that crazy long number like this (see below)…
14 billion + 350 million + 770,000 + 910 + 4
You’ll see that 7 cleanly goes into the first four terms. Thus all you’re left with is the 4 at the end.
Here are the answers:
1. 4
2. 15 and 60
3. A
4. B
5. D
6. C
can someone explain the 3 rd one(standard deviation)?Thanks in advance !
If you subtract (or add) the same number from (or to) every term in the set, the standard deviation does not change.
However, if you multiply (or divide) each term in the set by a number, the standard deviation changes by that amount.
In the first case, we are subtracting 4, so nothing changes.
In the second case, we’re multiplying by .95, resulting in a smaller standard deviation.
Thus we choose A
Hi, I’m not getting the 4th question (the probability one), if anyone could help?
I believe the key word here is “approximately”: \frac{{4 \choose 3} {8 \choose 3} }{ {12 \choose 6}} = 0.242424... \approx 0.25 = \frac{1}{4}
However, I don’t think it is practical to use combinations in the exam. Is there an easier way around that?
I took the same way as you did, got the answer \frac{8}{33} ,then I doubt if my approach was wrong. @gregmat any input here sensei?
Seems like that’s the correct answer. What approach did you take?
i would recommend using cfrac instead of frac in latex
cfrac \cfrac{1}{2}
frac \frac{1}{2}
basically like this
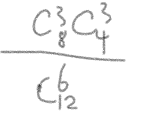
ahh thank you. I think cfrac is used in typing continued fractions
looks like cfrac can make it display bigger here
That’s how I did it
Can someone explain the second question?
Hi @shradha.saria, I didn’t attend the session and not sure if there is a faster way. @gergmat, can you let us know if there is a faster approach?
Here is how I did it.
Step 1: We can have 3, 4, or 5 consecutive integers. Let the first integer be x.
-
x, x+1, x+2
-
x, x+1, x+2, x+3
-
x, x+1, x+2, x+3, x+4
Step 2: compute the average of each of them:
-
\frac{x+x+1+x+2}{3} = \frac{3x+3}{3} = x+1
-
\frac{x+x+1+x+2+x+3}{4} = \frac{4x+6}{4} = x+\frac{6}{4}
-
\frac{x+x+1+x+2+x+3+ x+4}{5} = \frac{5x+10}{5} = x+2
Step 3: compute double the range for each of them:
-
2(x+2 - x) = 2(2) = 4
-
2(x+3 - x) = 2(3) = 6
-
2(x+4-x) = 2(4) = 8
Step 4: equate the two equations from step 2 and step 3, and solve for x. If it is not integer, then the choice is wrong.
-
x+1 = 4 \Rightarrow x = 3, an integer

-
x+\frac{6}{4} = 6 \Rightarrow x = 6 - 6/4 , clearly, not an integer

-
x+2 = 8 \Rightarrow x = 8 - 2 = 6 , an integer

Step 5: find the product of first and last integer
-
(x)\times(x+2) = 3 \times 5 = 15
-
(x)\times(x+4) = 6 \times 10 = 60
Very nicely formatted!
For Q5, is there any ‘definite’ algebraic method?
I counted back from 20, and realized that 17/3 leaves the same remainder as 17/5. And hence, 17/7 would leave a remainder of 3.
So is the strategy just to choose the correct number?
Also, these questions seem a bit harder. Are they GMAT level or current GRE?