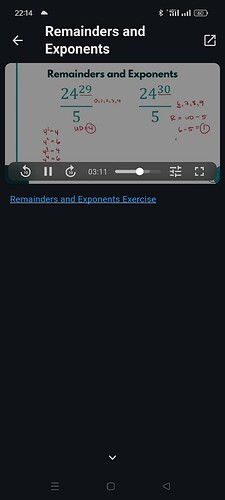
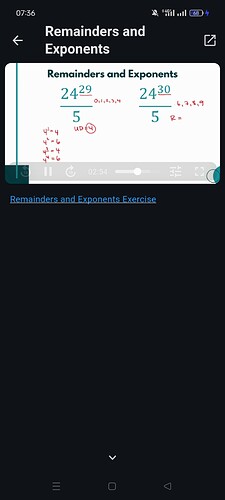
Need guidance regarding Remainder & exponents. Till remainder deux ,it was easy but after that I have noticed that the rules are different when it comes to remainder & exponents
Hi can you clarify further?
When to do consider unit digit and directly divide the numerator by denominator?? I have found that Greg in some maths did the divination and in some maths considered exponents
Just to clarify, we’re finding the remainder in all these cases - there is no real “division” going on. So for instance, in the last screenshot, we’re finding the remainder when 36^{17} is divided by 2.
That means you want to say I have to find unit digit, unit digit of 6 is 6 which will divide the exponent, the remainder will be the answer or again have to find which digit has that remainder as we did in remainder chapters? I don’t know whether I have made it clear or not, but the chapter is making me freak out
The question is asking what the remainder is, so that’s the answer…
Keep in mind that “unit digit” is not the same as “remainder”, except when you’re dividing the number by 10.
Just tell me I just have to divide the numerator with denominator & the remainder would be the answer? Exponent has nothing to do with it?
Exponent definitely has something to do with it. I think you’re missing the point.
Let’s try this: what is the remainder when say 5^{49} is divided by 3? Show your steps clearly.
Remainder is 2? After that what to do?
How did you get that?
5/3
By your logic, the remainder of 5^x (where x is a positive integer) should be 2 when divided by 3. Is that right?
Yea
And that’s where your logic fails, because that isn’t correct. The whole point of these kind of problems is to find a pattern.
Let’s try this with the previous example:
- The remainder when 5 is divided by 3 is 2
- The remainder when 5^2 = 25 is divided by 3 is 1
- The remainder when 5^3 = 125 is divided by 3 is 2
- The remainder when 5^4 = 625 is divided by 3 is 1
Do you see a pattern?
Oh that means in this math we have to at first divide the exponents of unit digit by the denominator in question?? Then what about 49?
No. We’re finding the pattern by explicitly calculating 5^1, 5^2, 5^3, … and finding the remainders for these (small) numbers - we can use the calculator for that after all. Then we use that to find a pattern we can use to solve the problem for larger powers of 5.
In my previous answer, can you notice that when x is even, the remainder of 5^x when divided by 3 is 1? What if x is odd? Can you use that to answer the question on the remainder of 5^{49} when divided by 3?
No, because exponent is 49, so answer would be 2??
Well yes, because 49 is odd, and we’ve established via the pattern that when x is odd, the remainder would be 2.
Can you now apply this to the original problem you gave in the question?
Thanks for clarification, U did it step by step that’s why, I understood, thanks a lot ![]()
![]()
![]()
![]()
![]()
![]()