Hello, in the video below, we’ve talked about replacement vs non replacement. My question is, with replacement, are the two events Pull 1 and Pull 2 independent or dependent?
With replacement, it is independent because the probability of pull 2 is not affected by pull 1.
However, in the case of without replacement, it is dependent because the probability of pull 2 is affected by pull 1.
Are you sure? The prepswift video says otherwise. It says that without replacement pull 2 is independent of pull 1, imagining as if it were a new bag before the second pull.
Yes, I’m sure. I mean the probability is altered by pull 1, so pull 2’s probability is altered and hence dependent on pull 1.
That makes sense.
@Leaderboard Could you please review the independent video on prepswift and take a look at this conversation? Thanks
What is the exact event we are looking at here (write it out even if it was previously written somewhere in the conversation)?
The first event is pulling out a red marble out of the bag; whereas the second event is pulling out a red marble out of the bag after having not replaced the red marble that was previously pulled out.
Is there a second possible answer to your second event (if not, where’s the dependency)? Recall that for independence, P(A \cap B) = P(A) \times P(B). Does that not hold in this case?
If we’re really being technically then you have to formally lay out your random experiment. Also the answer to your question depends wholly on your sample space.
I’ll distill it down so it’s still comprehensible, suppose you had two events:
Event 1 = pulling red first
Event 2 = pulling red second
These events are dependent if you have at least 2 red marbles and at least 1 marble of a different type. This is what we mentioned prior, albeit briefly.
Similarly, if your marble had exactly 2 red marbles in it and nothing else, then these events are independent because both events have probability 1.
More rigorously, imagine we have a bag with x red marbles and y blue marbles and x,y \geq 2. You then proceed to draw 2 marbles in order \& without replacement. The events are such that:
A = first draw is red
B = second draw is red
It’s easy to see that P(A) = P(B) = \frac{x}{x + y}, and now you can ask the question about whether these two events are independent.
P(A \cap B) = \frac{x(x-1)}{(x + y)(x + y - 1)}.
As in, is P(A \cap B) = P(A) \cdot P(B), and the conclusion you notice is that they’re not necessarily independent unless we have 0 of one marble type, which can’t happen because we supposed that we wanted each marble type to be \geq 2.
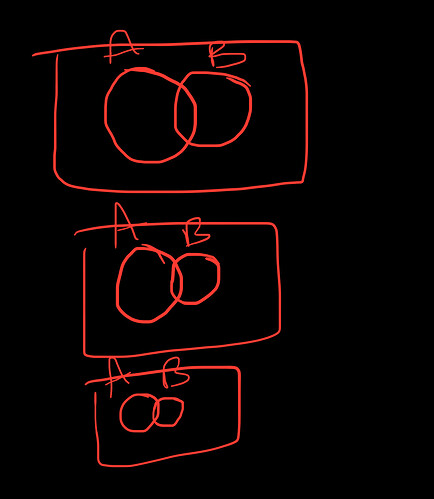
In pull 2, the bag has 4 red marbles rather than the initial 5, and 5 blue marbles. So, the second event (pull 2) could be either red or blue, but with lower probability for the red one as we threw out one red in the first pull. Hence, with no replacement, circle A (red) in Venn diagram has caused circle B (red) to become smaller. So, the first event A has led to having less occurrence of B in the second event. As a result, this situation doesn’t comply to the definition of independent events.
To answer your question, I’d say yes an overlap holds, but with a lower P(B) in the second event which was caused by no replacement
If we were to draw a venn diagram for the chain events of pulling a red marble with no replacement from the same bag, it would look like this. From the image, you can see that each pull affects the size of the subsequent pull. Yes, I concede that there is an overlap, which checks the first mark of the definition of independent events; however, there is a direct influence or effect that each event has on the other, which unchecks the second condition of independent events.
Again, the confusion seems from not properly defining what the second event is.
@cylverixxx is correct because they specifically use the following definition:
These two events are not independent and that user has clearly explained why. This does not appear to be what Greg is showing in the video - it appears to me that he is using this definition instead:
- Event 1: pulling red first
- Event 2: pulling red second given that the first pull is a red
Do you see the difference? Notice that P(A \cap B) = P(A) \times P(B) does hold in this case. Regardless, I’ll link this discussion to the video soon, because the question raised is legitimate.
Hello Leaderboard, thanks for your response. I am afraid to say that I still don’t see the difference between the 2 events you mentioned and the two events mentioned by Cylverxxx. Could you please use the Venn diagram in your explanation as it helps make things clearer. How would you label event 1 and event 2 in the example mentioned in the video? I am labeling them as follows:
First circle: pulling a red
Second circle: pulling a red as well
They’re basically the same; this was how it seemed in the video. I don’t remember hearing something about the order (first, second, third) in this particular example in the video.
This is still vague. I would label them like this:
In other words:
- P(event 1) = 5/10
- P(event 2) = 4/9
In cylverixxx’s case,
- P(event 1) = 5/10
- P(event 2) = 5/10 \times 4/9 + 5/10 \times 5/9
The reason is that if you say
this also includes the case where the first pull is NOT a red. However, in
The “given” part means that this is not possible.
I think now it’s started to make sense to me, although I am still unclear about the correlation between the algebraic equation you both mentioned and the conclusion you reached. It is very confusing to me.
For example:
Yes, I’ve started to see the difference. But how noticing this difference does lead us to conclude that P(A \cap B) = P(A) \times P(B)P(A∩B)=P(A)×P(B)P(A \cap B) = P(A) \times P(B) does hold in this case?
And again, the same confusion happened with Cylverxxx use of this equation here:
I didn’t get how from solely the above mentioned equations could lead to the conclusion that they are not independent.
To be honest, I don’t know what is wrong. Maybe this foundation is not clear enough in the prepswift video related to replacement vs non replacement. Is there an alternative video explaining this problem in the regular study plans?
Why are we multiplying 4/9 and 5/9 by 5/10 in each probability of event 2? In other words, why don’t we just say, P(event 2) = 4/9 + 5/9? Since Cylverxxx defined that event 2 is the probability of pulling a red second, shouldn’t we just add up the two cases that could happen with red, without counting the blue ones? I mean if you multiply by the probability of the blue marbles, you then get the total probabilities, not the red ones.
It holds in this one:
because
P(event 1 and event 2) is \frac{5}{10} \times \frac{4}{9} = P(event 1) \times P(event 2)
Try applying the above equation for cylverixxx’s case and see whether they hold. The P(A \cap B) = P(A) \times P(B) case for independence is a “iff” (if and only if) case - it holds both sides.
Lack of precision in the statements, coupled with Greg not being clear enough in the videos.
Because in their case, event 2 is
As a result, to answer this question, we need to consider two cases:
- when the first pull is red AND the second pull is red
- when the first pull is not red AND the second pull is red
Hence, we consider both cases separately and add them up to get the final probability.
In other words, why don’t we just say, P(event 2) = 4/9 + 5/9?
First, notice that by your implication, P(event 2) is 1 → you have a 100% chance of picking a red ball second, which is incorrect.
Also: the reason it does not hold goes back to why in cylverixxx’s case, the two events are not independent. We have two cases that ultimately lead to event 2 (them being the first pull being red and not red). The probability of these two “cases” aren’t equal - do you see the dependency there?
multiply by the probability of the blue marbles
We are not doing that?
Thanks Leaderboard for your thorough response. It almost clears my doubts on this problem. The last thing I wanted to ask about is this:
You don’t. However, if the equation holds, they are independent. So it works both ways.
Thanks Leaderboard and thanks Cylverxxx for your help. Much appreciated.