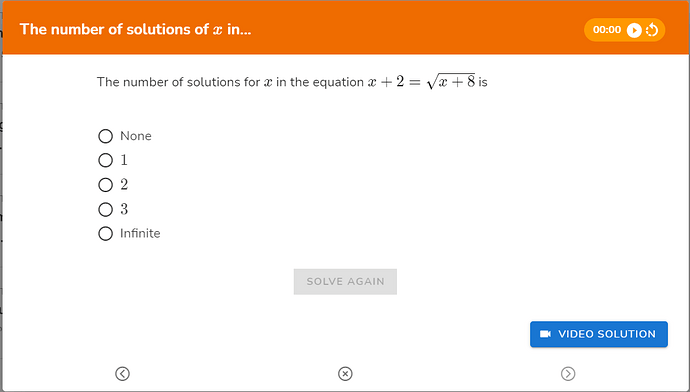
Why is -4 an invalid root for the equation? -2 is also a root of +4 right? Question is taken from the GRE Quant Problem Solving on Gregmat website.
(x+2)^2= x+8
x^2+4+4x=x+8
x^2-4+3x=0
x=1,-4
Now, verfying the solution
First : x =1
(x+2)= \sqrt{x+8}
(1+2)= \sqrt{1+8}
3=3
LHS = RHS
Second x = -4
(x+2)= \sqrt{x+8}
(-4+2)= \sqrt{-4+8}
-2\neq2
LHS \neq RHS
Thus, only x = 1 is our solution
1 Like