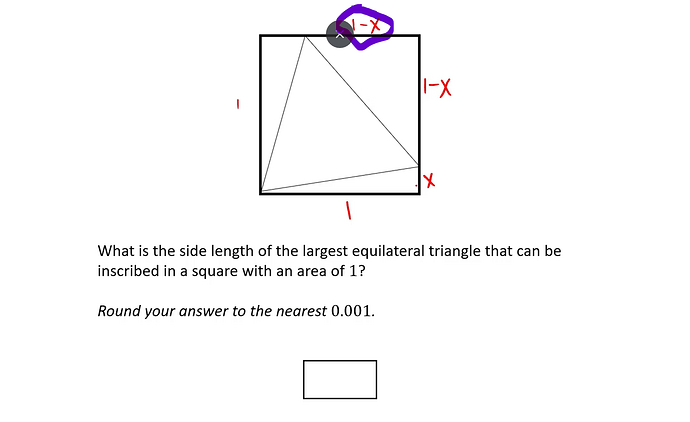
I didn’t understand in the solution - why on the top side of the square it is (1-x)? I understand that on the right hand side we assume part of the line to be x, making the the remaining part 1-x.
However, it is not implied in the question that the two vertices of the equilateral triangle that are not coinciding with the square corner, divide the two sides proportionally. Is this an implied assumption? is the reason behind it the fact we’re dealing with an equilateral triangle?