First foray attempting gregmat’s quant practice and I encountered a rather difficult one! I don’t even understand what I do not understand. Can a kind soul help to unpack it for me from the top pls? This is a total confidence killer after attempting quant reasoning and 5lbs ![]()
Essentially, we need to find a value g(x) which when substituted in f(x) would give us x^n (3rd equation), using the first two equations.
So, let’s suppose g(x) is x^n, then according to first equation f(g(x)) would be nx^(n-1), but we require it to be x^n. This can be achieved if we make g(x) to be x^(n+1). Then substituting g(x) = x^(n+1),
f(g(x)) = (n+1)x^n
x^n is correct, but we have (n+1) extra that we need to remove, for this we can use the second equation which says f(nx) = nf(x).
So, if g(x) = (x^(n+1))/(n+1), then f(g(x)) = x^n which is what we need in eqn 3.
Hence, Option C.
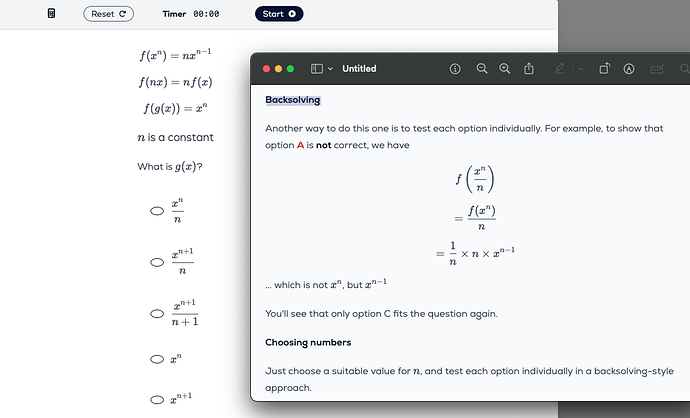
Other way of solving is to put the given options as g(x) in third equation and breakdown the equation using first two equations and see if they result in x^n, For example, checking for Option A,
Using equation 2, we can say,
f(x^n/n) = f(x^n)/n
And we know f(x^n) from the first equation, which will result in
f(x^n/n) = x^(n-1)/n
which is not equal to what we want in the third equation, hence Option A is wrong.