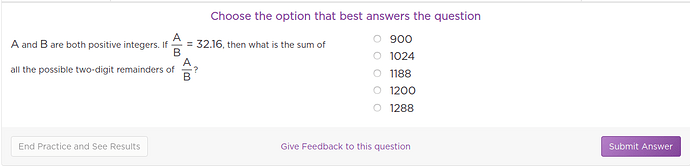
Fun question, so we know A/B = 32.16 , which can also be written as 32 + 16/100 = 32 + 4/25. This means that 4 is the remainder which when divided by 25 gives 0.16 as the latter part of the quotient with which we are concerned. Similarly we can also deduce that any multiple of 4 could be the remainder as well for instance, 16/100 where 16 is a multiple of 4.
Now, the question is asking sum of all possible two digit remainders of A/B. We know that multiples of 4 will be as 4,8,12,16…infinity, but we only need to concern ourselves with 2 digit remainders. Hence we are focused on the range from 12 to 96.
Finally this becomes an Arithmetic Progression problem, where a = 12, an = 96 & d = 4.
an = a +(n-1)d
96 = 12 + (n-1) 4
n = 84/4 +1 = 22.
Sum of n = (n/2) * (a + an) = (22/2) * (12 + 96) = 11 * 108 = 1188 = (c)
I couldn’t find a shorter method, let me know if anyone knows.
Hope this helps.
Jeet
Great! Thanks.