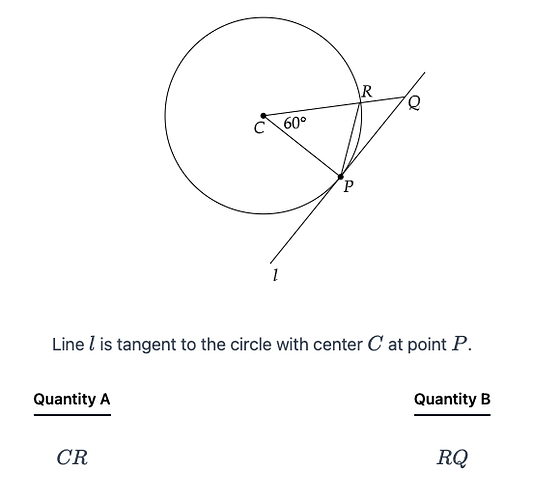
For this question I don’t get how in the solution because we know RQP = RPQ then we can deduce the PQ = RQ? Please can someone explain?
Sorry, it should be PR = RQ. This has been fixed in the solution.
Hello, please can you explain why? I get the angles are the same but why does that mean the 2 sides are the same?
I recommend revisiting the “Angle versus Side Length” video on PrepSwift.
What’s the answer & why?
The key to this question is that line l is tangent to the circle at point P. From the ETS Math Review: “If a line is tanget to a circle, then a radius drawn to the point of tangency is perpendicular to the tanget line”.
So to start solving this question - first fill out the angles that you know. \angle CPQ and \angle CRP are both 60^{\circ}. \angle PRQ is 180^{\circ} - 60^{\circ} = 120^{\circ} . Because l is tangent to the circle at point p, \angle RPQ is 90^{\circ} - 60^{\circ} = 30^{\circ}. This must mean that \angle RQP is also 30^{\circ} because the degrees to a triangle must add to 180^{\circ}.
To get the relationships of the sides we can look at the angles. Since \triangle CPR is equilateral and RQP = RPQ, it follows that CR is equivalent to RQ