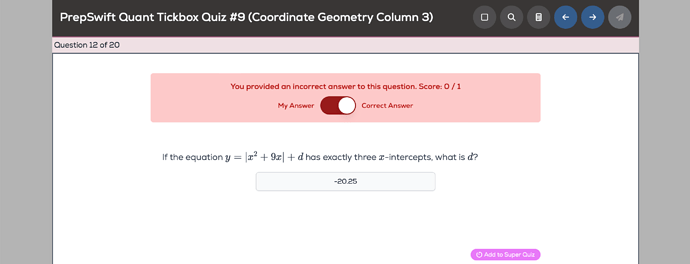
Can someone please explain why this is -20.25 not 20.25?
How did you get -20.25 in the first place?
2 equations:
- x^2+9x+d . if you use the discriminant we get 81 - 4(1)(d) . if d =81/4 the solution is 0 therefore 1 solution
- -x^2-9x+d. if we use the discriminant we get 81 - (4)(-1)(d). again if d=81/4 the solution is + therefore 2 solutions
My answer was 81/4 but the correct answer is -81/4
The problem stems from this:
Consider your first equation. You have
x^2 + 9x + d = 0
The problem is that this is true only when |x^2 + 9x| \geq 0. If you use the discriminant and get d = 81/4, the equation becomes
x^2 + 9x + \frac{81}{4} = 0
The roots of this is -4.5, which does not satisfy the x^2 + 9x \geq 0 condition, and hence fails.