Understanding Diagonal of the Square

GRE Quant Problem Solving
1

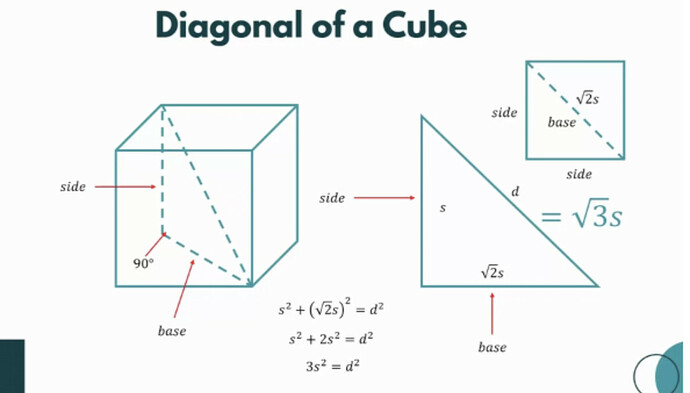
Hi esteemed forumers, I am struggling to breakdown the steps to identify the length of the diagonal of a cube. Can someone help?

So I understand that to find the diagonal length, the process entails:

  1. Finding the length of the base which is a hypotenuse of a 45-45-90 = (root 2).x
  2. The (root 2).x is the base of the diagonal line as part of the second 45-45-90… this is where I am stuck. I understand that if I use the Pythagoras theorem ie a^2 + b^2 = c^2 will help me to find the diagonal line but it should naturally work with the 45-45-90 technique, right? I couldn’t quite figure out why is it the diagonal is a (root 3)s unless the triangle is a 30-60-90? Is it because the side of the triangle is not the same as the base? but even then, the base should be (root 3) x s, where s = (root 2) s, and therefore the hypotenuse is (root 3) (root 2 multiplies with s)? Sorry quite convoluted there but hope someone can help to untangle it for me. Thank you in advance.

image
image1188×678 60.2 KB

2

You know the sides, but not the angle.

3

Eventhough it’s a cube, it’s not reasonable to deduce 45-45-90? But your explanation makes sense - that means to find the diagonal line the long way especially if there’s any tricky question, we should use the a^2 + b^2 = c^2. Otherwise, stick with (root 3)s.

4

It is not.

The \sqrt{3}x part only applies for 30-60-90 triangles. Don’t mix the two up.

5

Okay got it. For this diagonal thing, it’s purely Pythagoras theorem rather than the unique relationship of 30-60-90 and 45-45-90