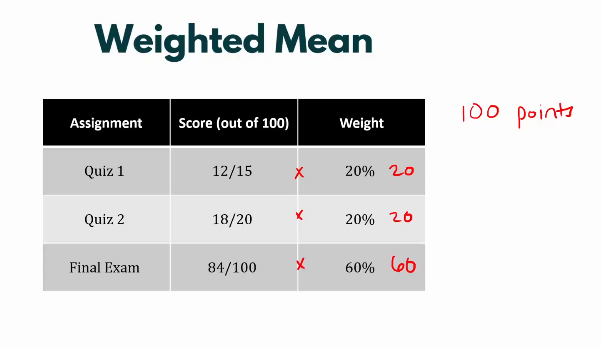
In this question, why are we multiplying say 12/15 with 20? If it carries 20% weightage, why can’t we do (20/100)12 ?
I thought that weighted averages= Value1 * Weight + Value2 * Weight/ Total weight
Where am I going wrong, please help.
Assuming a value just makes it easier to calculate weighted average. Instead of assuming 100, lets say the total points on the test were y.
Step 1: 20% of y = 0.2y , 60% of y = 0.6y
Step 2: Multiply the weights with their respective scores-
Formula of weighted average
=(0.2y12/15 + 0.2y18/20 + 0.6y*84/100)/ 0.2y + 0.2y + 0.6y
Step 3: Take y common so it cancels out
(0.2(12/15) + 0.2(18/20) + 0.6(84/100))/ 0.2 + 0.2 + 0.6
Note that denominator would be equal to 1 because they add up to 100%
solving the equation
Step 4:
0.16 + 0.18 + 0.504 = 0.844
Multiply this by 100 to see this in percentage form
Why Does Assuming 100 Work?
When weights are expressed as percentages (like 20%, 60%), assuming 100 makes calculations intuitive because y is essentially just a placeholder for “the total weight.” Since y cancels out, the final result is the same regardless of whether y=100, y=50, or y=1000.
In your example, 12/15 is one value so you can’t separate it out by multiplying it only by 12.
Let me know if this is what you wanted to ask or am I interpreting this incorrectly. It would also be great if someone from Greg mat team would confirm if this explanation is correct or not because that is how understood this concept. So, would be interested in knowing if this makes sense.
This is a great explanation, but my doubt still is that why is 12/15 one unit? doesn’t 12/15 mean that a person has scored 12 marks out of 15 and thus the score to be used for the weighted average should be 12?
Where am i going wrong?
When the question says “score is out of 100,” it means the weights for the final calculation are based on percentages (out of 100%). However, the actual scores for each quiz or test are still given relative to their individual maximums (e.g., Quiz 1 is out of 15, Quiz 2 is out of 20, Final Exam is out of 100).
Basically:
Scores (e.g., 12/15): These tell us how well the student performed relative to each individual test.
Weights (e.g., 20%, 60%): These tell us how much each test contributes to the final grade, as a percentage of the total grade.
The “out of 100” applies only to the weights, not to the raw scores directly. This is why we still need to use fractions like 12/15 or convert them to percentages (e.g., 12/15=80%) for calculating the weighted mean. Using “12” without considering the maximum score 15 would be misleading because the quizzes have different scales (e.g., Quiz 1 is out of 15, Quiz 2 is out of 20, Final Exam is out of 100) and if you ignore the scale and use “12” directly, you wouldn’t account for how well the person performed relative to the maximum possible score.