Suppose if we take k= 35 (the first option) then what is n ?

Where is this question from?
The final is answer will be the options for which \frac{-1+\sqrt{8.K^{2} + 1}}{2} will give an integer value (The expression is equal to n)
Greg’s question bank
This is how I approached it:
Concept tested = Consecutive integers (mean = median or \frac{\text{First term +last term}}{2})
Now, sum of k-1 integers will be \frac{1+(k-1)}{2}\text{median}\times (k-1)\text{-->Number of terms} \tag{1}
What have I trouble understanding is that in the series (k+1)+(k+2)......n, is it n being the last integer .
so sum will be \frac{(k+1)+n}{2}(\text{median}) \times (n-(k+1)+1)\text{-->Number of terms} \tag{2}
Now, if we equate equation 1&2, won’t we end up with \cancel{two-unknown-variables},\text{one variable} .
k^2=n^2+n \tag{3}
Ahh, we know k , so we have to input each answer then solve the quadratic equation and check if its right or wrong?
I think this question is screaming SKIP ME
Is there a shortcut that I am missing as this seems like a lot of work for 1 point?
Hi, there is no built in short cut at the moment. We just attended a class on this problem and Greg spent the hour talking about this one piece by piece.
Fantastic problem but yes it screamed the right thing at you, SKIP.
BTW, did someone asked him if they can expect such lengthy questions in the GRE now ?
Equation 2 seems wrong, I got the sum of RHS to be \frac{(n-k)(n+k+1)}{2} and the final equation would be n^2 + n = 2.k^2 and on simplifying for the positive root of x, you’ll arrive at the same equation as mentioned in my previous comment (But I approached that differently)
\frac{(k+1)+n}{2}(\text{median}) \times (n-(k+1)+1)\text{-->Number of terms} \tag{2}
I think its the same
The 2 was missed 
did you use the quadratic formula for getting to the final equation ? I personally don’t even remember it 
Yes, I did 
It’s quite the contrary for me. It’s etched in my mind 
What I did for my tests was just mug formulas a night before and breeze through it once more in the morning (putting that short term memory into use). For eg : when I first saw this question I immediately googled what was the formula for average when we got consecutive integers (Article), so I was looking if anyone got any choosing number or other trick .
“Never in a million years” replied the man. But the concepts that are blended are sure to appear in the test and someone who’s aiming for a 165+ should know them.
Meanwhile I was just content by figuring out the left hand side on my own but the person who figured out the right hand side had my mind effing blown.
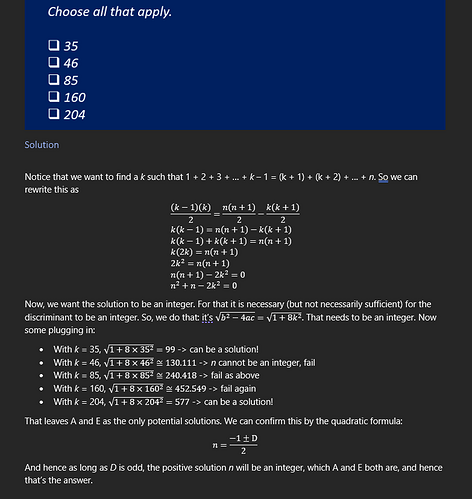
This is not an easy question. But this was the reference solution while the question was being produced in the factory (click to expand):
I see, instead of solving the full quadratic formula you’re just solving a part of it to save some more time .
After watching greg’s solution video, I still can’t get it. Does anyone here have a better explanation? And I didn’t get why he assumed that the first k-1 integers are consecutive.
First 10 integers would mean: 1,2,3,4,5,6,7,8,9,10 (Although I do think that first 10 POSITIVE integers should be mentioned)
And these are consecutive numbers
I was able to solve this question, but it turned out to be the same method as Greg’s
I can help with a particular step, but don’t have an alternative method in mind